[챌린지]머신러닝 스킬업 - 임영재 튜터님 4회차
챌린지 4회차
[수업 목표]
- 스마트 팩토리 데이터(삼성 스마트팩토리)를 활용한 데이터 분석
[목차]
- 다중공선성 처리 방법
- 다중공선성이란?
- VIF기반 변수제거
- 높은 상관관계를 가진 변수 제거
- PCA 분석
- 정규화 회귀
- 결측치처리
- 결측치 제거
- 평균,중앙값, 최빈값 대체
- KNN Imputation (K-최근접 이웃 대체)
- 다중 대체법 (Iterative Imputation, MICE)
- 이상치처리
01. 다중공선성 처리 방법
- 다중공선성이란?
- 독립 변수(Feature)들 간에 강한 상관관계가 있는 경우를 의미
- 선형 회귀 모델에서는 다중공선성이 있으면 계수(Weight) 추정이 불안정해지고, 해석이 어려워짐 ✅ 그렇다면? 선형 모델이아닌 비선형모델에서는 다중공선성 처리가 필요한가? ⇒ 비선형 모델(랜덤 포레스트, XGBoost, 신경망 등)은 선형 모델과 다르게 다중공선성의 영향을 받지 않거나, 적게 받는 경향이 있음→ 변수 간의 독립성을 가정하지 않으며, 다중공선성이 있어도 트리가 분할할 변수를 자동으로 선택하기 때문에 영향이 적음 하지만, 비선형 모델에서도 다중공선성이 문제될 수 있는 경우
- 불필요한 변수가 많아져 모델의 복잡도가 증가(과적합)
- 모델 해석(Feature Importance)이 왜곡될 가능성
- 훈련 데이터 효율성 저하
- 랜덤 포레스트, XGBoost 같은 트리 기반 모델
- 다중공선성이 심할 경우 모델 성능을 저하시킬 수 있으므로 적절한 처리가 필요
- VIF기반 변수제거
✔️ 개념:
- VIF(Variance Inflation Factor) 값이 높으면 해당 변수는 다른 변수들과 높은 상관관계를 가짐
- 일반적으로 VIF 값이 10 이상이면 다중공선성이 높다고 판단하고 제거 고려
✔️ 방법:
- 모든 변수에 대해 VIF를 계산
- VIF 값이 가장 높은 변수를 제거하고 다시 VIF 계산
- VIF 값이 10 이하가 될 때까지 반복
높은 상관관계를 가진 변수 제거
✔️ 개념:
- 피어슨 상관계수를 계산하여 상관계수 0.9 이상인 변수 쌍 중 하나를 제거
✔️ 방법:
- 피어슨 상관행렬을 계산
- 상관계수가 0.9 이상인 변수 쌍을 찾음
- 도메인 지식이나 모델 성능을 고려하여 제거할 변수를 결정
PCA 분석
✔️ 개념:
- 다중공선성이 높은 변수를 직접 제거하지 않고, 새로운 축으로 변환하여 차원을 줄이는 방법
- PCA(Principal Component Analysis)를 사용하여 주요 정보를 유지하면서 변수를 축소
예제: 2개의 강한 상관관계를 가진 변수 X, Y가 있을 때
- X, Y 두 개의 변수를 사용하지 않고, X와 Y를 합친 새로운 축(PC1)을 만든다.
- X와 Y의 중복 정보를 제거하면서도, 전체적인 데이터의 변동성을 최대한 유지한다.
✔️ 방법:
- 주성분 개수(n_components)를 결정
- PCA를 적용하여 새로운 변수로 변환
- 변환된 변수를 모델에 사용
✅ 이점:
- 다중공선성을 해결하면서도 데이터의 정보를 최대한 유지
- 모델이 변수를 학습하는 데 효율적
🚨 주의:
- PCA 적용 후 해석력이 떨어질 수 있음
- 변수 중요도를 직접 해석하기 어려움
정규화 회귀
✔️ 개념:
- 다중공선성이 있는 데이터에서 변수를 제거하지 않고 모델 학습 시 페널티를 부과하여 해결
- Lasso 회귀는 일부 변수를 완전히 제거, Ridge 회귀는 모든 변수를 유지하면서 가중치를 감소
✔️ 사용 경우:
- 다중공선성을 해결하되, 변수를 제거하지 않고 싶을 때
- 선형 회귀 모델을 사용할 경우
02. 결측치 처리
결측치 제거
✔️ 개념:
- 결측값이 포함된 행(row) 또는 열(column)을 제거하는 방법
✔️ 사용 경우:
- 결측치가 매우 적고, 제거해도 데이터 손실이 크지 않은 경우
- 해당 칼럼이 분석에서 중요하지 않을 경우
평균,중앙값, 최빈값 대체
✔️ 개념:
- 결측치를 해당 칼럼의 평균(mean), 중앙값(median), 최빈값(mode)으로 대체하는 방법
- 연속형 변수(숫자)에는 평균/중앙값, 범주형 변수(문자)에는 최빈값을 사용
✔️ 사용 경우:
- 데이터가 정규 분포를 따를 경우 → 평균
- 이상치가 많거나 비대칭 분포를 가질 경우 → 중앙값
- 범주형 데이터 → 최빈값
KNN Imputation (K-최근접 이웃 대체) #많이 사용
✔️ 개념:
- 결측값이 있는 샘플과 가장 유사한 샘플(k개)을 찾아 평균값을 사용하여 결측치를 채우는 방법
✔️ 사용 경우:
- 연속형 데이터에서 패턴이 있을 때
- 데이터 간의 유사성이 높을 때
다중 대체법 (Iterative Imputation, MICE)
✔️ 개념:
- 다른 변수들과의 관계를 고려하여 반복적인 예측을 통해 결측값을 채우는 방법
- 여러 번 반복하면서 결측치를 점진적으로 보완함
✔️ 사용 경우:
- 데이터가 연속형이고, 다른 변수들과의 관계가 있을 때
03. 이상치 처리
이상치 제거
✔️ 개념:
- 이상치를 감지한 후, 해당 값을 포함하는 행(row)이나 열(column)을 삭제하는 방법
✔️ 사용 경우:
- 이상치가 센서 오류, 입력 실수 등으로 발생했으며 실제 의미가 없는 경우
- 이상치가 전체 데이터의 1~5% 이하로 매우 적을 때
- 이상치가 불량과 관련되지 않은 경우
이상치를 경계값으로 대체
✔️ 개념:
- 이상치 값을 최대/최소 경계값(Q1 - 1.5×IQR, Q3 + 1.5×IQR)로 대체하는 방법
✔️ 사용 경우:
- 이상치를 제거하면 데이터 손실이 클 경우
- 이상치가 극단적인 값이지만 완전히 무시할 수는 없을 때
로그 변환, Box-Cox 변환
✔️ 개념:
- 데이터의 분포가 한쪽으로 치우쳐 있거나 이상치가 큰 값을 가질 때, 로그 변환(Log Transform) 또는 Box-Cox 변환을 사용하여 이상치의 영향을 줄임
✔️ 사용 경우:
- 데이터가 비대칭 분포일 때
- 이상치를 직접 제거하지 않고, 데이터 변환을 통해 해결하고 싶을 때
- 데이터의 범위 차이가 너무 커서 이상치가 모델에 영향을 줄 때
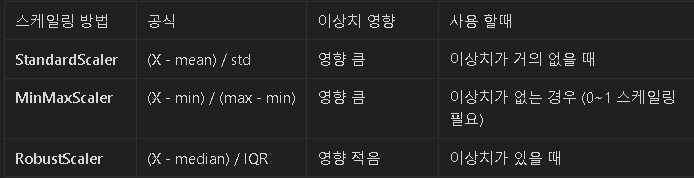
RobustScalingc # 이상치 처리보단 정규화에 가까움
✔️ 개념:
- 평균(mean) 대신 중앙값(median), 표준편차(std) 대신 IQR(Interquartile Range, 사분위 범위)을 사용하여 데이터를 변환하는 방법
- 이상치(outlier)가 있는 데이터에서도 이상치의 영향을 최소화하면서 데이터를 스케일링할 수 있음
🔹 왜 Robust Scaling을 사용할까?
✅ 이상치가 있는 경우에도 변환이 안정적임
✅ 데이터의 전체적인 분포를 유지할 수 있음
✅ 특정 변수의 값이 너무 크거나 작아서 스케일 차이가 클 때 유용함
🚨 주의:
- Robust Scaling은 비율 기반 변환이므로 데이터의 분포가 크게 변하지 않음
- 하지만 극단적으로 이상치가 많으면 성능이 떨어질 수도 있음
KNN Imputation
✔️ 개념:
- 이상치 값을 비슷한 샘플(k개)의 평균값으로 대체하는 방법
✔️ 사용 경우:
- 이상치가 존재하지만, 해당 값이 완전히 잘못된 것이 아닐 때 (도메인 지식 기반)
칼럼 추가
예시 1) 이상치 여부를 나타내는 새로운 변수(_outlier_flag)를 추가하여 모델이 이를 학습하도록 함 이상치 자체가 중요한 패턴을 나타낼 수 있을 때 (예: 특정 이상치가 불량과 관련이 있을 경우)
이상치 = 불량 =>
예시 2) 이상치 플래그와 특정 센서 데이터를 조합하여 새로운 변수(feature)를 생성 특정 센서값이 이상일 때 불량률이 증가하는 경우
어떤 방법을 써야하는가?
1️⃣ 이상치가 오류라고 확신되면?
→ ✅ 이상치 제거 (Filtering, Dropping)
2️⃣ 이상치를 제거하기 어렵다면?
→ ✅ Winsorization (경계값 대체)
3️⃣ 데이터가 한쪽으로 치우쳐 있다면?
→ ✅ 로그 변환 or Box-Cox 변환
4️⃣ 이상치의 영향을 줄이면서 정규화하고 싶다면?
→ ✅ Robust Scaling
5️⃣ 이상치를 다른 값으로 자연스럽게 보완하고 싶다면?
→ ✅ KNN Imputation
6️⃣ 이상치 자체가 중요한 정보라면?
→ ✅ 이상치 플래그 추가
📢 즉, 이상치를 단순히 제거하는 것이 아니라, 데이터 특성과 분석 목표에 따라 적절한 방법을 선택하는 것이 중요함 🚀
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
[베이직] 파이썬 핵심 쏙쏙 - 손보미 튜터 4회차
베이직 4회차
[수업 목표]
- 데이터분석에서 사용하는 기초 통계 개념을 숙지합니다.
- 다양한 예제 실습을 통해서 통계 코드를 실습합니다.
[목차]
- 베이직 - 파이썬 핵심 쏙쏙 수업 일정
- 지난 시간 복습과제 풀이
- 회귀 분석
- 정규성
문제 2번 (정답지 오류 있음)
10월,11월,12월이 1월로 잘림
-> 인덱싱 하려면 2018년_1월을 2018년_01월 로 수정해야함 나중에 ㅇㅇ
* .idxmax()
해당 데이터 인덱스에서 가장 큰 인덱스를 알려줌
문제 3번
* 문자열.zfill(n): 문자열의 길이를 n으로 맞추고, 부족한 부분은 앞에 0을 채워주는 함수. ‘신고시각’ , ‘출동시각’ 칼럼을 zfill(6)를 활용하여 적절한 형식으로 변환해야 합니다.
3. 회귀 분석
회귀분석 개요
- 정의: 독립변수(원인)가 종속변수(결과)에 미치는 영향을 분석하는 방법.
- 활용 분야:
- 가격 예측 (부동산, 주식 등)
- 수요 예측 (상품 판매량)
- 머신러닝 기반 예측 모델링
단순 선형 회귀 (Simple Linear Regression) # 못씀 쓸일이 없음
- 독립변수 1개 → 종속변수 예측
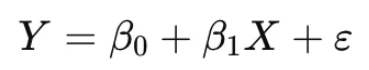
- Y: 종속변수 (예측값)
- X: 독립변수
- β0: 절편 (Intercept)
- β1: 기울기 (Slope)
- ε: 오차 (Residual)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 예제 데이터 (공부 시간 vs 시험 점수)
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([50, 55, 65, 70, 80])
# 선형 회귀 모델 학습
model = LinearRegression()
model.fit(X, y)
# 예측값 계산
y_pred = model.predict(X)
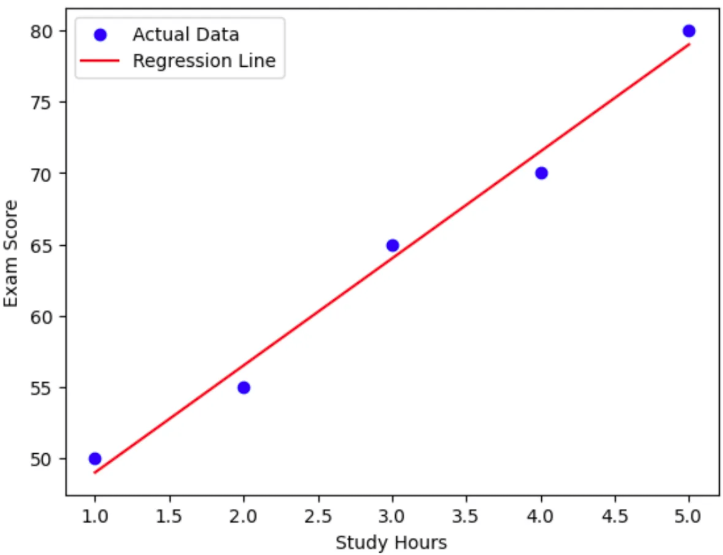
# 그래프 시각화
plt.scatter(X, y, color='blue', label="Actual Data")
plt.plot(X, y_pred, color='red', label="Regression Line")
plt.legend()
plt.xlabel("Study Hours")
plt.ylabel("Exam Score")
plt.show()
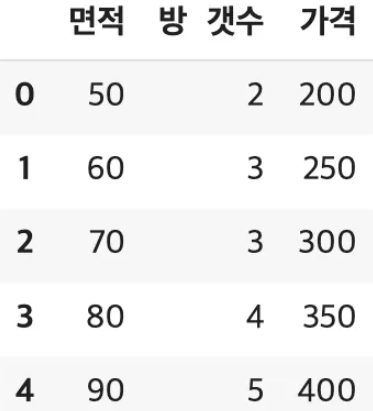
다중 선형 회귀 (Multiple Linear Regression)
- 독립변수 여러 개 → 종속변수 예측
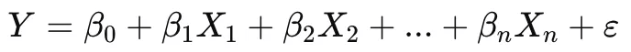
from sklearn.linear_model import LinearRegression
# 예제 데이터 (면적, 방 개수 -> 집값 예측)
X = np.array([[50, 2], [60, 3], [70, 3], [80, 4], [90, 5]])
y = np.array([200, 250, 300, 350, 400])
df=pd.DataFrame(X,columns=["면적","방 갯수"])
df["가격"]=y
model = LinearRegression()
model.fit(X, y)
print("회귀 계수:", model.coef_)
print("절편:", model.intercept_)
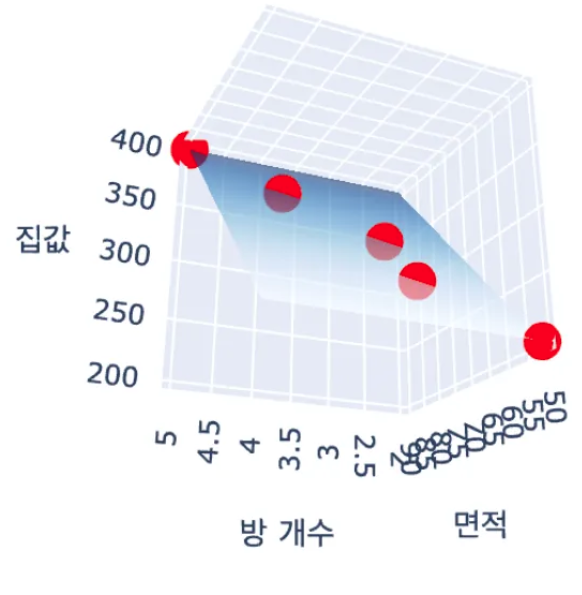
import plotly.graph_objects as go
import numpy as np
# 예측할 그리드 생성
x0, x1 = np.meshgrid(np.linspace(50, 90, 10), np.linspace(2, 5, 10))
y_pred = model.predict(np.c_[x0.ravel(), x1.ravel()]).reshape(x0.shape)
# 3D 그래프
fig = go.Figure(data=[
go.Scatter3d(x=X[:, 0], y=X[:, 1], z=y, mode='markers', marker=dict(size=6, color='red'), name="실제 데이터"),
go.Surface(x=x0, y=x1, z=y_pred, colorscale="Blues", opacity=0.6, name="회귀 평면")
])
fig.update_layout(title="다중 선형 회귀 - 집값 예측", scene=dict(xaxis_title="면적", yaxis_title="방 개수", zaxis_title="집값"))
fig.show()
회귀 모델 평가 지표
✅ 1.결정계수 R^2
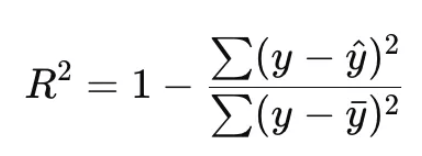
- 모델이 데이터를 얼마나 잘 설명하는지를 나타냄. 0~1 사이의 값을 가짐
- 1에 가까울수록 설명력이 높음.
✅ 2.오차 기반 지표 (Error-based Metrics)
- 예측값과 실제값의 차이(오차)를 기반으로 평가하는 지표들.
- 값이 작을수록 성능이 좋다.
✅ 2.1 MSE (Mean Squared Error, 평균 제곱오차) # MAE는 안쓰임
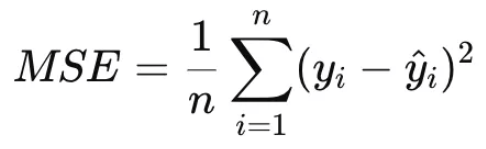
- 특징: 오차(Residual)를 제곱하여 평균을 구한 값, 기본적인 오차지표 # 이상치 영향 많이 받아 잘못씀
- 장점: 큰 오차에 민감해서 큰 오차를 강조함 (이상치 영향 O)
- 단점: 오차의 크기가 제곱되므로 해석이 어려움 (단위 문제)
- 적합한 경우: 이상치(outlier)를 강조하고 싶을 때, 일반적인 상황에서 가장 많이 사용됨
from sklearn.metrics import mean_squared_error, r2_score
mse = mean_squared_error(y, y_pred)
rmse = np.sqrt(mse)
r2 = r2_score(y, y_pred)
print("MSE:", mse)
print("RMSE:", rmse)
print("R^2:", r2)
** 변수 없음 그냥 흐름만 이해
✅ 1.2. RMSE (Root Mean Squared Error, 평균제곱근오차)
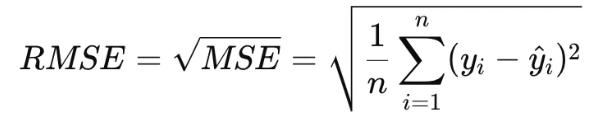
- 특징: MSE의 단위를 맞추기 위해 제곱근을 씌운 값
- 장점: 단위가 원래 y와 동일해 해석이 쉬움
- 단점: 여전히 이상치에 민감함
- 적합한 경우: 실제 값과 같은 단위로 오차를 보고 싶을 때, 예측값이 큰 경우 사용
✅ 1.3. RMSLE (Root Mean Squared Logarithmic Error, 평균제곱로그오차)
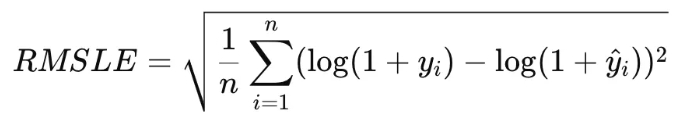
- 특징: 로그 변환 후 RMSE 계산, 작은 값과 큰 값의 상대적 차이를 강조
- 장점: 작은 값에 대한 오차를 상대적으로 강조하며, 이상치의 영향을 줄임
- 단점: 음수 값 사용 불가, 로그 변환으로 인해 해석이 어려울 수 있음
- 적합한 경우: 예측값이 상대적인 비율 차이를 갖는 경우 (예: 판매량/수요량/매출/인구수 예측에 적합)
- 예를 들어, 자영업자의 식료품 재고 예측을 위한 주제에서, 2종 오류(주문량보다 식료품을 적게 주문하는 경우, 과소예측) 에 더 큰 패널티를 부과하기 위해 RMSLE를 선택
✅ 3. 상대 오차 지표 (Relative Error Metrics)
- 예측값과 실제값의 상대적인 차이를 평가하는 지표
✅ 3.1. MAPE (Mean Absolute Percentage Error, 평균절대백분율오차)
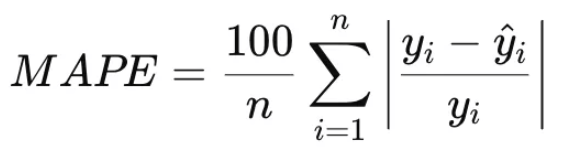
- 특징: 오차를 **비율(%)**로 나타내기 때문에 해석이 쉬움
- 장점: 값의 크기에 관계없이 상대적인 오차를 확인 가능
- 단점: y 값이 0에 가까울 때 불안정해짐
- 적합한 경우: 상대적인 예측 오차가 중요한 경우 (예: 매출, 가격 예측)
로지스틱 회귀 (Logistic Regression)
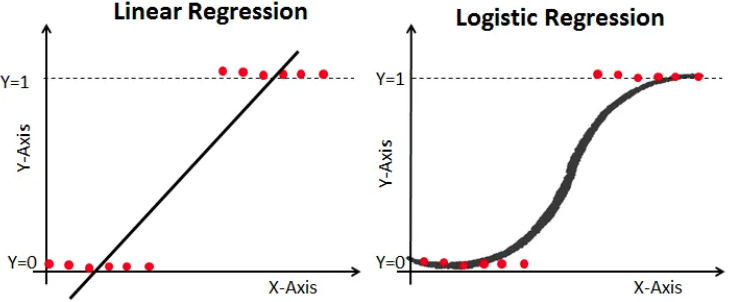
✅ 개념
- 선형 회귀와 다르게 이진 분류(참/거짓) 문제를 해결하는 방법.
- 출력값이 확률(0~1) 범위로 변환됨.
- 시그모이드(Sigmoid) 함수 적용:
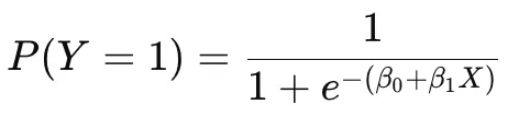
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
# 예제 데이터 (공부시간 vs 합격 여부)
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
y = np.array([0, 0, 0, 1, 1]) # 0: 불합격, 1: 합격
# 로지스틱 회귀 모델 학습
model = LogisticRegression()
model.fit(X, y)
# 특정 공부 시간(3.5시간)에 대한 합격 확률 예측
pred_prob = model.predict_proba([[3.5]])
print(f"공부시간 3.5시간일 때 합격 확률: {pred_prob[0][1]:.4f}") # 0.4791
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
import koreanize_matplotlib
# 시그모이드 곡선을 그리기 위한 x값 생성
X_test = np.linspace(0, 6, 100).reshape(-1, 1)
y_pred = model.predict_proba(X_test)[:, 1]
# 그래프 그리기
plt.figure(figsize=(8, 6))
# 시그모이드 곡선 그리기
plt.plot(X_test, y_pred, 'g-', label='로지스틱 회귀 곡선')
# 실제 데이터 포인트 표시
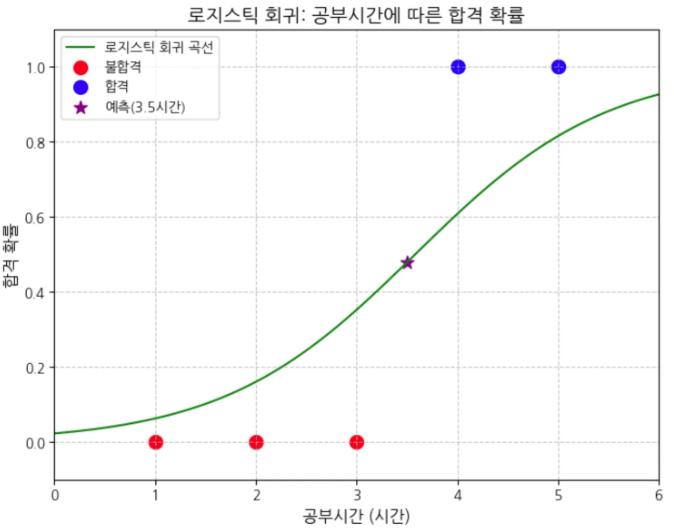
plt.scatter(X[y==0], y[y==0], color='red', label='불합격', s=100)
plt.scatter(X[y==1], y[y==1], color='blue', label='합격', s=100)
# 3.5시간 예측값 표시
pred_prob = model.predict_proba([[3.5]])
plt.scatter(3.5, pred_prob[0][1], color='purple', label='예측(3.5시간)', s=100, marker='*')
# 그래프 꾸미기
plt.title('로지스틱 회귀: 공부시간에 따른 합격 확률', fontsize=14)
plt.xlabel('공부시간 (시간)', fontsize=12)
plt.ylabel('합격 확률', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend()
# 축 범위 설정
plt.xlim(0, 6)
plt.ylim(-0.1, 1.1)
plt.show()
print(f"공부시간 3.5시간일 때 합격 확률: {pred_prob[0][1]:.4f}")
OLS(Ordinary Least Squares)
- 회귀분석의 F-test (전체 회귀 모형의 유의성을 검정) - 선형인지 아닌지
- 귀무가설: 회귀 계수들은 모두 0이다 -> 선형이 아니다
- 대립가설: 적어도 하나의 회귀 계수는 0이 아니다. -> 선형이다
- 회귀분석의 t-test (개별 회귀 계수의 유의성을 검정)
- 독립변수와 종속변수 간 선형적인 연관이 없다
- 대립가설: 독립변수와 종속변수가 선형적인 연관이 있다.
윈도우) 파일- 추가기능- 분석도구 추가
OLS(Ordinary Least Squares) summary
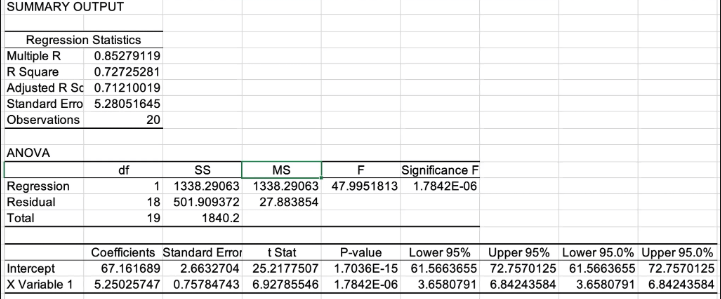
R Square (결정계수): 0.7273 (72.73%)
공부시간(독립변수)이 시험점수(종속변수) 변동의 72.73%를 설명함
Adjusted R Square: 0.7121 (71.21%)
변수의 수를 고려한 수정된 결정계수로, 실제 설명력을 더 정확하게 나타냄
F-검정 (회귀모델의 전체 유의성): F값: 47.9952
Significance F (p-value): 1.7842E-06 (0.0000017842)
해석: p-value가 0.05보다 매우 작으므로, 회귀모델이 통계적으로 매우 유의함
t-검정 (개별 변수의 유의성)
X Variable 1 (공부시간)
계수(β): 5.2503
공부시간이 1시간 증가할 때 시험점수는 평균 5.25점 증가
t Stat: 6.9279
P-value: 1.7842E-06
해석: p-value가 0.05보다 매우 작아 공부시간과 시험점수 간 유의미한 선형관계가 있음
95% 신뢰구간: [3.6581, 6.8424]
공부시간 1시간 증가 시 점수 상승 효과가 95% 확률로 이 구간 안에 있음
절편(Intercept)
값: 67.1617
P-value: 1.7036E-15
해석: 공부시간이 0일 때의 예상 시험점수는 약 67.16점
95% 신뢰구간: [61.5664, 72.7570]
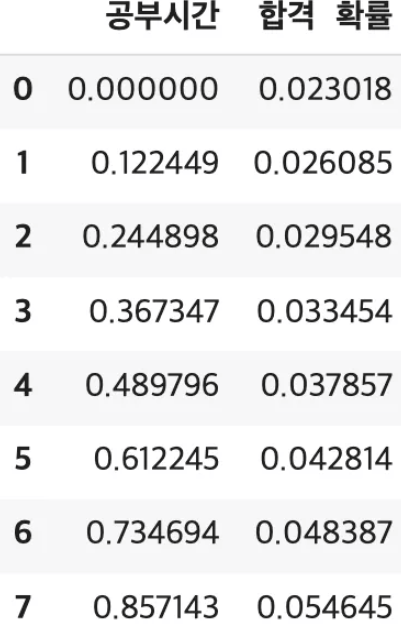
4. 정규화 (Normalization)
데이터 분포확인
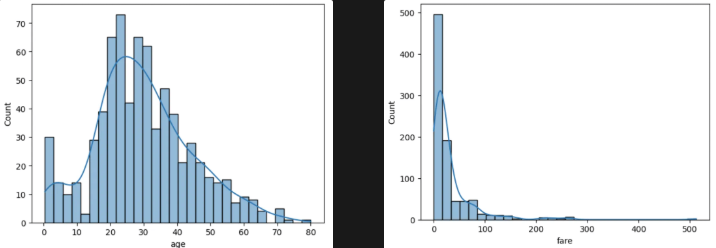
- 타이타닉의 ‘age’, ‘fare’ 칼럼을 이용해서 실습을 진행해보겠습니다.
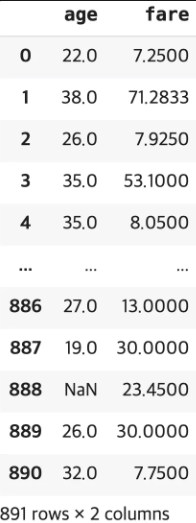
1. 히스토그램
- 히스토그램은 데이터의 분포를 시각적으로 표현하는 그래프입니다.
import seaborn as sns
sns.histplot(df['age'], bins=30, kde=True) # bins: 막대 갯수, kde=True 곡선그래프 넣어
sns.histplot(df['fare'], bins=30, kde=True)
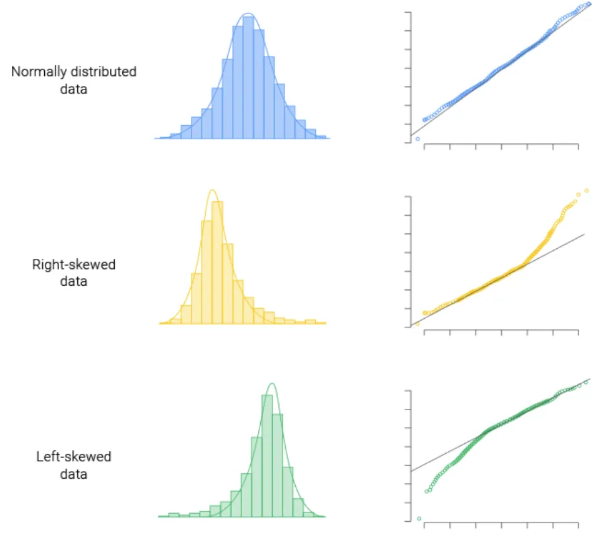
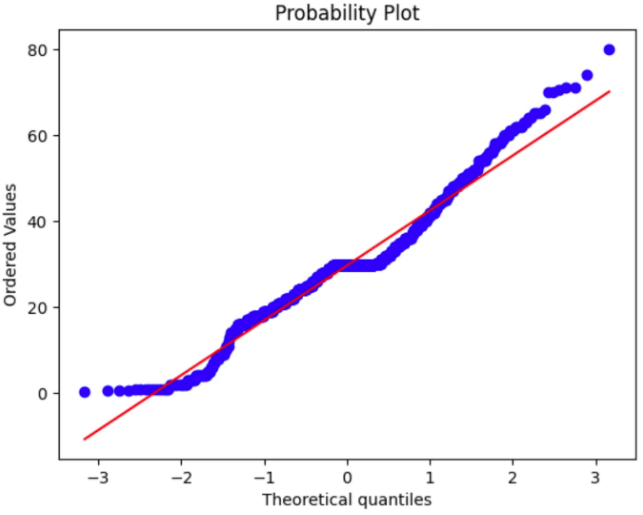
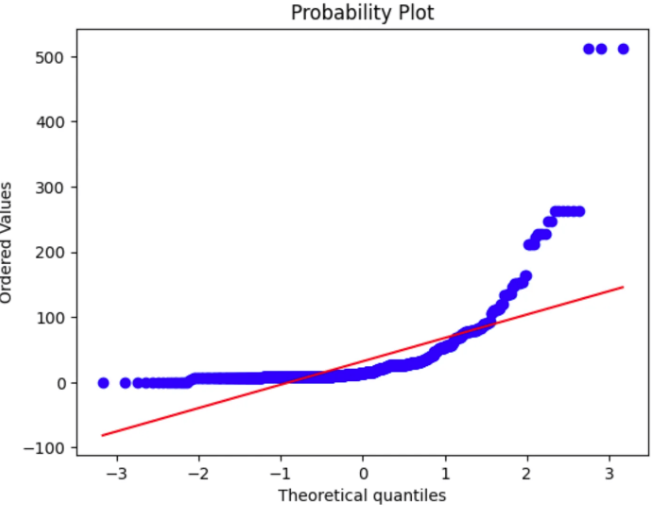
2. Q-Q plot
- q-q plot은 데이터가 정규분포를 따르는지 확인하는 그래프로, 점들이 대각선에 가까울수록 정규성을 만족한다고 볼 수 있다.
import seaborn as sns
import matplotlib.pyplot as plt
import scipy.stats as stats
# age칼럼의 Q-Q plot
df['age'].fillna(df['age'].mean(),inplace=True)
stats.probplot(df['age'], plot=plt)
# fare칼럼의 q-q plot
stats.probplot(df['fare'], plot=plt)
plt.show()
스케일링
**데이터 스케일링(Data Scaling)**이란 수치형 변수에서 서로 다른 변수의 값 범위를 일정한 수준으로 맞추는 작업입니다.
정규화 종류
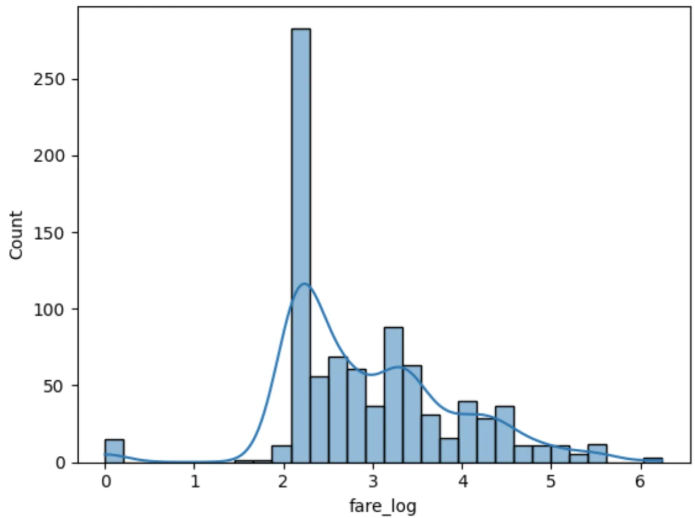
1) 로그 변환 (Log Transformation)
데이터분포가 비대칭 (positively skewed) 일 경우 적합
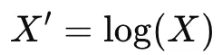
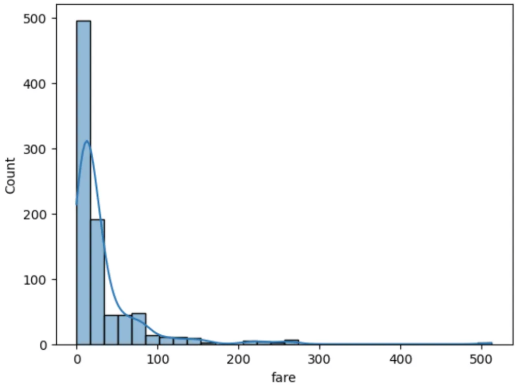
shift transformation : 로그함수는 0 값에서는 정의되지 않으므로, 변수에 1을 더한 뒤, 로그변환 (Box-Cox 변환도 사용 가능)
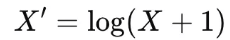
import numpy as np
df['fare_log'] = np.log1p(df['fare']) # log(1 + X) 사용
df[["fare","fare_log"]]
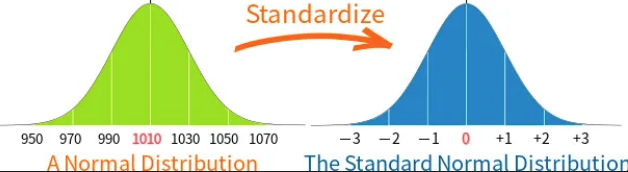
2) Z-점수 정규화 = 표준 정규화 (Z-score Normalization, Standardization, Standard Scaler)
평균을 0, 표준편차를 1로 변환, 가우시안 정규분포를 가진 값으로 변환
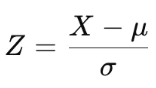
- X: 원본 데이터
- μ: 평균
- σ: 표준편차
from sklearn.preprocessing import StandardScaler
titanic = sns.load_dataset("titanic")
df=titanic[["age","fare"]]
# StandardScaler 객체를 생성합니다.
standard_scaler = StandardScaler()
standard_scaler.fit(df)
scal_t=standard_scaler.transform(df)
# fit_transform()으로 한 번에 변환 가능
#scal_ft=standard_scaler.fit_transform(scal)
standard = pd.DataFrame(scal_t, columns=df.columns)
standard.head()
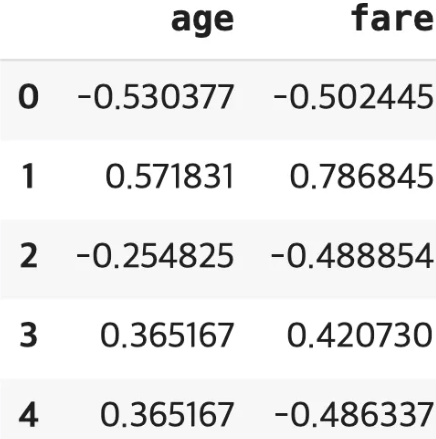
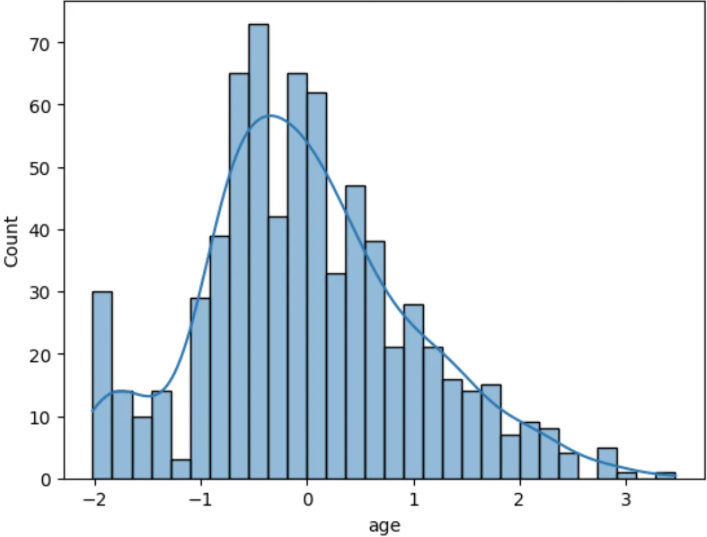
sns.histplot(standard["age"], bins=30, kde=True)
3) 최소-최대 정규화 (Min-Max Normalization) #데이터 0~1사이로 변환
데이터를 특정 범위 (0~1) 로 변환, 회귀 문제에 적합
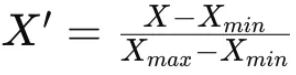
from sklearn.preprocessing import MinMaxScaler
titanic = sns.load_dataset("titanic")
df=titanic[["age","fare"]]
# 스케일러 객체를 생성합니다.
minmax_scaler = MinMaxScaler()
mm_ft=minmax_scaler.fit_transform(df)
minmax = pd.DataFrame(mm_ft, columns=df.columns)
minmax.head()
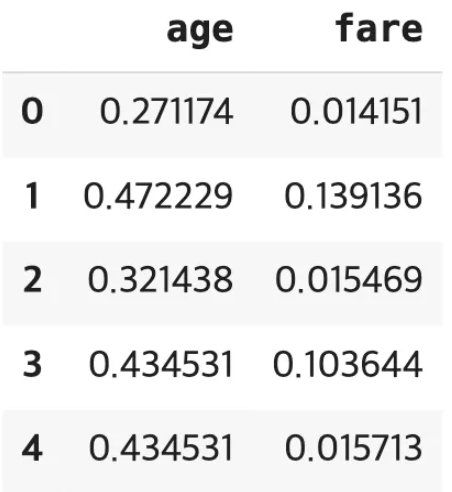
4) 로버스트 정규화 (Robust Normalization) #median을 중심으로 종모양
중앙값과 IQR 사용, 표준정규화 비해 이상치의 영향을 덜 받음
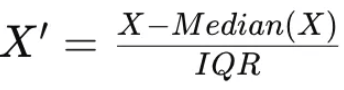
from sklearn.preprocessing import RobustScaler
titanic = sns.load_dataset("titanic")
df=titanic[["age","fare"]]
# RobustScaler 객체를 생성합니다.
robustScaler = RobustScaler()
r_ft=robustScaler.fit_transform(df)
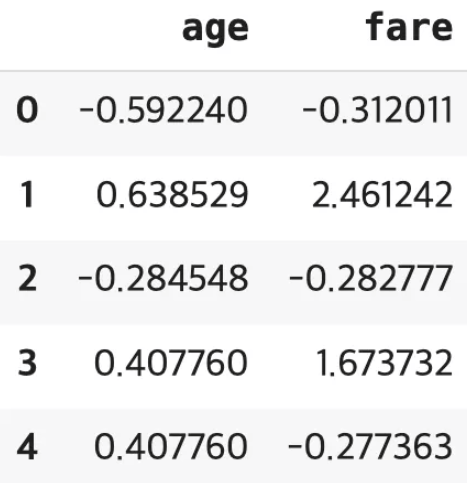
robust = pd.DataFrame(r_ft, columns=df.columns)
robust.head()
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
코드카타
코딩테스트 연습 - 3진법 뒤집기 | 프로그래머스 스쿨
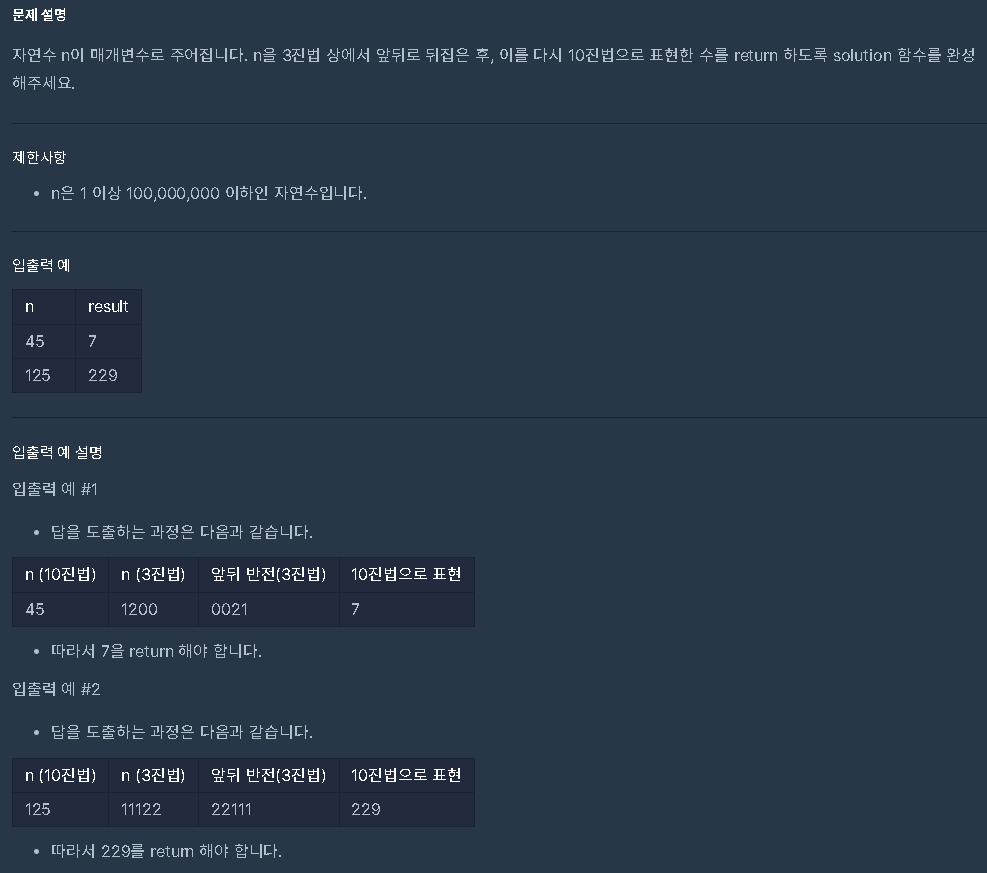
사이트 참고
파이썬 진수변환(2진법, 3진법, 5진법, 10진법)[n진법]
def solution(n, q):
rev_base = ''
while n > 0:
n, mod = divmod(n, q)
rev_base += str(mod)
return rev_base[::-1]
답은 출력되는데 애초에
def solution(n): 이 기본임
답지를 볼 순 없으니 도전
divmod(x, y) = (x // y, x % y)n.mod(v) = n%v
정답
def solution(n):
rev_base = ' '
while n > 0:
n, mod = divmod(n, 3)
rev_base += str(mod)
return int(rev_base,3)
정답 풀이
1. rev_base는 3진수로 변환된 값을 뒤집어서 저장할 문자열 변수
2, while 루프 : n을 3진수로 변환하는 과정
while n > 0:
n, mod = divmod(n, 3)
rev_base += str(mod)
divmod(n, 3)에서 n을 3으로 나눈 몫을 n에 다시 할당하고, 나머지를 mod에 할당
나머지 mod는 3진수의 한 자리에 해당하는 값이므로, 이를 rev_base
이렇게 반복해서 n이 0이 될 때까지 나머지를 구하고 이를 뒤집어 rev_base에 담습니다.
3. 3진수 뒤집기
- rev_base는 3진수 숫자들을 뒤에서부터 저장하고 있습니다. 예를 들어, n이 5일 때:
- 첫 번째 나누기: divmod(5, 3) → 몫: 1, 나머지: 2 → rev_base = ' 2'
- 두 번째 나누기: divmod(1, 3) → 몫: 0, 나머지: 1 → rev_base = ' 21'
결과적으로, rev_base는 3진수로 표현된 값인 '21'이 됩니다.
4. 3진수 문자열을 다시 10진수로 변환
return int(rev_base, 3)
rev_base는 이제 뒤집힌 3진수 값이므로, int(rev_base, 3)을 통해 이를 다시 10진수로 변환
예시
입력값이 n = 45일 경우:
- 45를 3으로 나누면 divmod(45, 3) → 몫: 15, 나머지: 0 → rev_base = ' 0'
- 15를 3으로 나누면 divmod(15, 3) → 몫: 5, 나머지: 0 → rev_base = ' 00'
- 5를 3으로 나누면 divmod(5, 3) → 몫: 1, 나머지: 2 → rev_base = ' 002'
- 1을 3으로 나누면 divmod(1, 3) → 몫: 0, 나머지: 1 → rev_base = ' 0021'
따라서 rev_base = ' 0021'이 되고, 이를 3진수로 해석하면 10진수로 7이 됩니다.
요약
- n을 3진수로 변환하고 그 숫자들을 뒤집습니다.
- 그 뒤집힌 3진수를 다시 10진수로 변환하여 반환합니다.
이 함수의 핵심은 숫자를 3진수로 변환한 뒤, 그 숫자들의 순서를 뒤집고, 그 결과를 다시 10진수로 변환하는 것입니다.
다른 사람 풀이
def solution(n):
tmp = ''
while n:
tmp += str(n % 3)
n = n // 3
answer = int(tmp, 3)
return answer1. 변수 초기화 tmp = ' '
2. 3진수로 변환
while n:
tmp += str(n % 3)
n = n // 3
이 부분은 n을 3진수로 변환하는 과정입니다. 반복문을 통해 n을 3으로 나누며 나머지를 구하고, 그 나머지를 tmp에 추가합니다.
- n % 3은 n을 3으로 나눈 나머지를 반환합니다. 이 나머지는 3진수에서 해당 자리에 들어갈 숫자입니다.
- n = n // 3은 n을 3으로 나눈 몫을 n에 다시 할당하여, 반복문을 계속 진행할 수 있도록 합니다.
반복문은 n이 0이 될 때까지 계속됩니다. 예를 들어, n이 5일 경우:
- 5 % 3 = 2이므로 tmp에 '2'가 추가됩니다.
- 5 // 3 = 1이므로 n은 1로 바뀌고, 다시 3으로 나누기를 시작합니다.
- 1 % 3 = 1이므로 tmp에 '1'이 추가됩니다.
- 1 // 3 = 0이므로 반복문이 종료됩니다. ### 그냥 while n: 만 적었는데 자동으로 n이 0이 되면 끝나네?
-> 처음 n은 정수로 기입했는데 0은 정수가 아니라(+실수도) False -> 자동break
결과적으로 tmp는 '21'이 됩니다. 이 값은 5를 3진수로 변환한 결과입니다.
3. 3진수 문자열을 다시 10진수로 변환
answer = int(tmp, 3)
tmp는 3진수로 표현된 숫자들의 순서가 뒤집힌 문자열입니다. 이 문자열을 int(tmp, 3)을 사용해 3진수로 해석하고, 이를 10진수로 변환합니다. 예를 들어, tmp = '21'이면, 이 값은 3진수로 '21'을 뜻하며, 이를 10진수로 변환하면 7이 됩니다.
4. 결과 반환
return answer
예시
입력값이 n = 5일 경우:
- 5 % 3 = 2, tmp = '2', n = 5 // 3 = 1
- 1 % 3 = 1, tmp = '21', n = 1 // 3 = 0
따라서 tmp = '21'이 되고, 이를 3진수로 해석하여 10진수로 변환하면 int('21', 3)은 7이 됩니다. 그래서 함수는 7을 반환합니다.
요약
이 함수는 다음과 같은 단계를 수행합니다:
- n을 3진수로 변환하여 그 값을 tmp에 저장.
- 그 뒤집힌 3진수를 다시 10진수로 변환하여 결과를 반환.
핵심은 숫자를 3진수로 변환한 뒤 그 값을 뒤집고, 뒤집어진 값을 다시 10진수로 변환하는 과정입니다.
코딩테스트 연습 - 이상한 문자 만들기 | 프로그래머스 스쿨
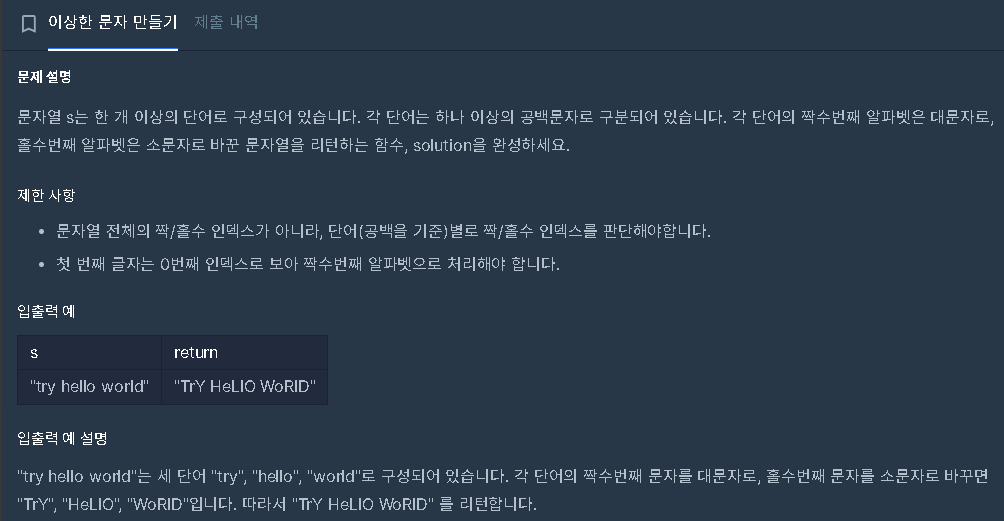
len(s) ## 15
s[3] ## ' '
s[0] ## 't'
오류
정답 -> 제출 후 채점에서 막힘
제한 사항
- 문자열 전체의 짝/홀수 인덱스가 아니라, 단어(공백을 기준)별로 짝/홀수 인덱스를 판단해야합니다.
- 첫 번째 글자는 0번째 인덱스로 보아 짝수번째 알파벳으로 처리해야 합니다.
공백 기준으로 짝/홀수 판단이네
내일하자 ㅇㅇ
'본 캠프 TIL' 카테고리의 다른 글
| 2월 11일 TIL 프로젝트 완료 (0) | 2025.02.11 |
|---|---|
| 2월 10일 TIL 파이썬 핵심 쏙쏙 5회차,[챌린지]머신러닝 스킬업 5회차 (0) | 2025.02.10 |
| 2월 6일 TIL 코드카타 (0) | 2025.02.06 |
| 2월 5일 TIL 코드카타 (0) | 2025.02.05 |
| 2월 4일 TIL [ML] 주요 기법 마스터 클래스 5회차,심화 프로젝트 발제, 코드카타 (0) | 2025.02.04 |