통계학 기초 라이브 세션 2차 - 정강민 튜터님
*파이썬 틀
1. 라이브러리
2. 데이터 불렁오기
3. 데이터 전처리
4. 모델 불러오기
5. 모델 실행 -> .fit() 메소드 사용
6. 실행 및 확인 -> 귀무가설과 대립가설과 p-value 머시기
[수업 목표] 제조업 예시 위주
- 생산·품질 데이터를 활용하여 통계적 실험(공정 비교, 개선 효과 검증 등)을 이해한다.
- 대표적인 통계적 실험 기법(예: 공정 전·후 비교)을 통해 가설 설정과 p-value 개념을 익힌다.
- 실제로 t-검정, 카이제곱검정 같은 통계적 검정 방식을 숙지한다.
- Python 라이브러리를 활용하여 검정통계량과 p-value를 계산하는 방법을 배운다.
* t-검정(평균 비교-2요인 t검정, 3요인 ANOVA분석)
1. 통계적 실험이란?
1) 정의
- 통계적 실험: 특정 개선 목적(“불량률 저감” 등)을 가지고, 표본으로부터 얻은 측정값(데이터)을 통계적으로 해석하여 결과(개선 효과가 유의한지)를 판단하는 과정
2) 목적
- 제한된 표본으로부터 전체(모집단)의 특징을 확률적으로 추론하기 위함
- 모든 제품을 전수검사하기 어렵거나, 모든 조건을 전부 테스트할 수 없을 때, 표본 검사를 통해 “진짜”(모집단) 상태를 추정하는 원리
3) 쉬운 예시
- “새 공정을 적용하면 불량률을 2% 이하로 내릴 수 있다.”
- 모든 제품을 전수검사하기 어려우므로, 일부만 뽑아 실제로 개선 효과가 ‘우연이 아닌지’ 판단
2. 품질관리자의 통계적 실험
DOE(실험설계), 제조업 현장에서 자주 활용
- 가설 설정
- 예: “개선 공정 도입 시 생산시간이 단축된다” (대립가설)
- 반대: “차이가 없다” (귀무가설) <- 확인하고 싶은것
- 실험 설계
- 공정 전(기존 방식)과 공정 후(개선된 방식)을 비교하기 위해, 시료·측정 방식·기간 등을 결정
- 데이터 수집
- 일정 개수의 제품을 무작위로 추출하거나, 일정 기간 생산 데이터를 수집
- 결과 해석
- 검정통계량과 p-value를 사용하여 “이 차이가 우연인지, 통계적으로 유의한 차이인지” 확인
* 현직에서는 데이터 수집을 SQL을 통해 함
-> 회사에 데이터 베이스 구축되어 있음 이를 SQL 가공을 통해 데이터 컬럼들을 불러오고 이를 통해 데이터 분석을 시작함
(데이터 규모가 어마어마함)
* 일반적인 방법
만약 컬럼 20개를 가지고 분석을 시작할 때 먼저 데이터 확인
-> 일단 시각화하여 방향성을 수립
-> 방향성을 바탕으로 가설 설정
-> 시각화에 넣어봤자 컬럼 3-4개 넣을 수 있는데 어떤 컬럼을 중점적으로 시각화에 넣을 것인지 결정해야함
-> 어떤 컬럼들이 중점적인지 확인하기 위해 ex) 상관관계를 분석해 히트맵으로 시각화해 중점적인 컬럼 선정
+ 통계학적으론 p-value값이 높은 것 위주로 방향성을 선정할 수도 있음
3. 분석 기법 선택하기
데이터 유형(범주형 vs. 연속형)에 따라 적절한 통계검정을 고른다.
- 연속형(시간, 무게, 길이 등)
- 2개(컬럼) 집단 평균 비교: t-검정, z-검정
- 3개(컬럼) 이상 집단 평균 비교: ANOVA(F-검정)
- 공통점 - 평균을 비교함
- ex ) 화장품 팩 a,b,c를 팔았는데 평균에 차이가 있으면 유의미하고 차이가 없으면 무의미함
- -> a,b,c를 ANOVA검정을 통해 p-value값을 확인해봄
- 범주형(불량/양품, 합격/불합격 등)
- 2개 이상의 집단에서 비율(또는 빈도) 비교: 카이제곱검정($\chi^2$)
예시
- T 검정: 공정 전/후(명목형x)의 평균 불량 개수(수치형y1), 평균 생산시간(수치형y2) 등(연속형)을 비교할 때
- 카이제곱검정: 공정 전/후(명목형x1)의 불량o/x(명목형x2,범주형)을 비교할 때 -> 독립성검정, 서열 비교할 때 쓰임
4. 평가 : 유의수준(α)과 신뢰수준(1−α)
1) 유의수준(α) 보통 5%
- “실제로는 차이가 없는데(귀무가설이 맞는데), 우연으로 기각해버릴 확률”
- 보통 0.05(5%) 사용 → 신뢰수준은 95%
2) 예시 해석
- α=0.05일 때, 만약 p-value < 0.05면 → “이 정도 차이는 우연이라 보기 힘들다”= 통계적으로 유의미
- p-value ≥ 0.05면 → “우연일 가능성이 높아” = 귀무가설(차이 없음)을 기각할 근거가 부족 , 귀무가설 채택
* 통계 돌렸을 때 p-value값이 0.05 이하일 경우 유의미 하다
5. 가설 채택 : p-value
1) p-value(확률값)
- “지금 관측한 차이가 우연히 발생할 확률”
- p-value < α → 대립가설 채택(차이 있음) , 통계적으로 유의미하다
- p-value ≥ α → 귀무가설 채택(차이 없음)
6. 공정 전/후 비교 실습 예시
import scipy.stats as st
import numpy as np
# 예: 공정 전/후 불량(참/거짓) 개수(범주형) → 카이제곱검정 or 이항검정 적합.
# 하지만 여기선 간단히 t검정으로 예시:
before = [0, 1, 0, 0, 2, 1, 1, 1, 0, 2] # 공정 전 불량 개수(10번 측정)
after = [0, 0, 0, 1, 0, 1, 0, 0, 0, 1] # 공정 후 불량 개수(10번 측정)
t_stat, p_val = st.ttest_ind(before, after)
print("검정통계량(t):", t_stat, ", p-value:", p_val)
alpha = 0.05
if p_val < alpha:
print("→ 귀무가설 기각 (개선 효과 유의미)")
else:
print("→ 귀무가설 채택 (개선 효과 통계적으로 확인 어려움)")
주의 불량 개수는 범주형 특성이 강해 카이제곱검정이나 Fisher의 정확검정이 실제론 더 적절할 수 있습니다.
핵심은 p-value 해석이며, $\alpha$=0.05와 비교해 결론을 내린다는 점은 동일합니다.
7. 오늘의 요약
- 통계적 실험: 공정 개선 여부(타겟값)(효과 유무)를 표본 데이터로 확인
- 가설 설정:
- 귀무가설(H0) = “차이 없음”, 대립가설(H1) = “차이 있음”
- 유의수준(α=0.05)과 p-value 개념
- p-value < 0.05 → “통계적으로 의미 있는 차이”
- 검정 방식:
- t-검정: 연속형 데이터(2집단) 비교
- 카이제곱검정: 범주형(불량/양품 등) 비교 (다음 세션에서 설명)
- ANOVA(F-검정): 3개 이상 그룹 평균 비교 등
- Python 라이브러리 활용
- scipy.stats를 사용하여 검정통계량과 p-value를 쉽게 계산
결론적으로, 업무에서 “새로운 설비/방법이 정말 효과 있는가?”를 객관적으로 판단하기 위해 통계적 검정(t검정, 카이제곱검정 등)을 활용하며, 그 결과를 p-value와 유의수준을 통해 해석한다는 점이 핵심입니다.
8. 실습으로 다지기
1. 실습 목표 정의
- 가설 설정: 연구 문제를 바탕으로 가설을 설정합니다.
- 예: "주중 평균 출근 시간은 8시간 이상이다."
- 통계적 유의성: 데이터를 통해 가설을 검증하고 신뢰 수준(예: 95%)을 설정합니다.
- 가설검정: 데이터를 바탕으로 귀무가설과 대립가설을 검정합니다.
2. 데이터 준비
예제 데이터: 직원들의 하루 평균 출근 시간(단위: 시간)

3. 가설 설정
- 귀무가설 (H₀): 주중 평균 출근 시간은 8시간 이하이다.
- 대립가설 (H₁): 주중 평균 출근 시간은 8시간 이상이다.
4. 통계적 유의성 설정
- 유의수준(α): 0.05 (95% 신뢰 수준)
5. 가설검정 절차
(1) 데이터의 기초 통계량 확인
- 평균: 데이터의 평균 출근 시간을 계산합니다.
- 표준편차: 데이터의 변동성을 측정합니다.
(2) 검정 방법 선택
- t-검정: 모집단의 표준편차를 모를 때, 평균에 대한 단일표본 t-검정을 사용합니다.
(3) 검정 수행
- 단일표본 t-검정을 사용하여 실제 평균이 8시간과 유의하게 다른지 판단합니다.
6. 파이썬 실습코드
import numpy as np
from scipy.stats import ttest_1samp
# 데이터
data = [8.1, 7.8, 8.2, 7.9, 8.0]
# 귀무가설: 평균 = 8
population_mean = 8
# t-검정 수행
t_stat, p_value = ttest_1samp(data, population_mean)
# 결과 출력
print("t-통계량:", t_stat)
print("p-값:", p_value)
# 유의 수준 비교
alpha = 0.05
if p_value < alpha:
print("귀무가설을 기각합니다: 평균 출근 시간이 8시간 이상 입니다.")
else:
print("귀무가설을 채택합니다: 평균 출근 시간이 8시간과 통계적으로 유의미한 차이가 없습니다.")
7. 결과 해석 (확정적인 결론이 아닌 보충적인 결론이라 이후 추가적인 다른 분석이 뒷받침 되야함)
- t-통계량: 귀무가설과 실제 데이터 평균의 차이를 정량적으로 나타냄.
- p-값: 귀무가설이 맞다는 전제 하에, 관찰된 데이터보다 극단적인 데이터가 나올 확률.
- p < α : 귀무가설을 기각.
- p≥α : 귀무가설을 채택.
******** 예시가 빈약함 시펄
8. 실습 확장
- 다른 검정 적용:
- 두 집단 간 비교 → 독립표본 t-검정
- 분포가 정규분포가 아닐 경우 → 비모수 검정(Mann-Whitney U Test)
- 데이터 확장:
- 모집단이 더 큰 경우, 샘플링 및 데이터 시각화.
- 실제 사례 적용:
- 제조 공정 데이터, A/B 테스트 데이터, 고객 설문조사 데이터 등.
필요하다면 데이터를 더 준비하거나 가설 설정을 확장해보세요! 😊
실습 매우 좋은 자료들임
실습 참고자료 1 : https://colab.research.google.com/drive/1AqG9YVXEU9sLCnLgh1sTZfluC7hAcORn?usp=sharing
실습 참고자료 2 : https://colab.research.google.com/drive/1tdBgmMsHfHUqHjMWaILcWrV9b39Si4de?usp=sharing
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
통계학 기초 3,4 주차 정리
3주차 유의성검정
[수업 목표]
★ 각각의 유의성 검정 방법들에 이해하고 특징을 파악한다
유의성 검정 종류
1) A/B 검정: 두 버전(A와 B) 중 어느 것이 더 효과적인지 평가(+비교)하기 위해 사용되는 검정 방법
- 마케팅, 웹사이트 디자인 등에서 많이 사용됨.
- 사용자들을 두 그룹(x1, x2)으로 나누고, 각 그룹에 다른 버전(A,B)을 제공한 후, 반응을 비교.
- 일반적으로 전환율, 클릭률, 구매수, 방문 기간, 방문한 페이지 수, 특정 페이지 방문 여부, 매출 등의 지표를 비교.
2) 가설검정
- 표본 데이터를 통해 모집단의 가설을 검증하는 과정
- 즉, 데이터가 특정 가설을 지지하는지 평가하는 과정
- 귀무가설(H0)과 대립가설(H1)을 설정하고, 귀무가설을 기각할지를 결정
- 데이터 분석시 두가지 전략을 취할 수 있음
- 확증적 자료분석
- 미리 가설들을 먼저 세운 다음 가설을 검증해 나가는 분석
- 탐색적 자료분석(EDA)
- 가설을 먼저 정하지 않고 데이터를 탐색해보면서 가설 후보들을 찾고 데이터의 특징을 찾는 것
- 확증적 자료분석
3) t검정: 두 집단 간의 평균 차이가 통계적으로 유의미한지 확인하는 검정 방법
- 독립표본 t검정과 대응표본 t검정으로 나뉨
☑️ 독립표본 t검정
- 두 독립된 그룹의 평균을 비교
☑️ 대응표본 t검정
- 동일한 그룹의 사전/사후 평균을 비교
4) 다중검정
- 여러 가설을 동시에 검정할 때 발생하는 문제
- 각 검정마다 유의수준을 조정하지 않으면 1종 오류(귀무가설이 참인데 기각하는 오류) 발생 확률이 증가
- 1종 오류가 무엇인지랑 왜 다중검정시 발생확률이 증가하는지는 밑에서 다시 설명! 지금은, 어떤 오류가 발생할 수 있다는 정도로 이해!
5) 카이제곱검정
- 범주형 데이터의 표본 분포가 모집단 분포와 일치하는지 검정(적합도 검정)하거나
- 두 범주형 변수 간의 독립성을 검정(독립성 검정)
* 범주형 - o,x / 수치형 - 1,2,3..
★ 신뢰구간과 가설검정의 관계에 대해 설명할 수 있다
- 신뢰구간과 가설검정은 밀접하게 관련된 개념
- 둘 다 데이터의 모수에 대한 정보 (ex. 평균) 를 구하고자 하는 것이지만 접근 방식이 다름
- 신뢰구간
- 특정 모수가 포함될 범위를 제공
* 신뢰구간 (Confidence Interval)
- 신뢰구간은 모집단의 평균이 특정 범위 내에 있을 것이라는 확률을 나타냅니다.
- 일반적으로 95% 신뢰구간이 사용되며, 이는 모집단 평균이 95% 확률로 이 구간 내에 있음을 의미합니다.
- 만약 어떤 설문조사에서 평균 만족도가 75점이고, 신뢰구간이 70점에서 80점이라면, 우리는 95% 확률로 실제 평균 만족도가 이 범위 내에 있다고 말할 수 있습니다.
* 가설검정
- 모수가 특정 값과 같은지 다른지 테스트
★ 제 1종 오류와 2종 오류에 대해 이해하고 구분할 수 있다

* Null hypothesis :귀무 가설
제 1종 오류 - 귀무가설이 참일 때 기각하는 오류
제 2종 오류 - 귀무가설이 거짓일 때 기각하지 않는 오류
+++++추가 이해 필요 (1.17.01:39)
+++ 이해중 .. (1.17.19:05)
++ 혈 뚫림 ㅈㅈ (1.17.20:22)
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
3.1 A/B 검정 #두 그룹 (A, B)과 비교하는게 포인트!
1) A/B 검정
- A/B 검정은 두 버전(A와 B) 중 어느 것이 더 효과적인지 평가하기 위해 사용되는 검정 방법.
- 마케팅, 웹사이트 디자인 등에서 많이 사용됨.
- 사용자들을 두 그룹으로 나누고, 각 그룹에 다른 버전을 제공한 후, 반응을 비교.
- 일반적으로 전환율, 클릭률, 구매수, 방문 기간, 방문한 페이지 수, 특정 페이지 방문 여부, 매출 등의 지표를 비교.
☑️ 목적
- 두 그룹 간의 변화가 우연이 아니라 통계적으로 유의미한지를 확인.
2) A/B 검정이 실제로 어떻게 적용되어질까?
- 온라인 쇼핑몰에서 두 가지 디자인(A와 B)에 대한 랜딩 페이지를 테스트하여 어떤 디자인이 더 높은 구매 전환율을 가져오는지 평가.
- ☑️ 두 개를 비교하여 구매 전환율이 큰 것을 선택
import numpy as np
import scipy.stats as stats
# 가정된 전환율 데이터
# 참고. 이항분포 생성 (예: 한번의 실험 - 동전 던지기 10회 반복 / 앞면이 나올 확률 0.5 / 총 1000번의 실험횟수)
# binom_dist = np.random.binomial(n=10, p=0.5, size=1000)
group_a = np.random.binomial(1, 0.30, 100) # 30% 전환율
group_b = np.random.binomial(1, 0.45, 100) # 45% 전환율
# t-test를 이용한 비교
t_stat, p_val = stats.ttest_ind(group_a, group_b)
print(f"T-Statistic: {t_stat}, P-value: {p_val}") # f ' ', f " " 이거 나중에 현업에서 겁나 잘 써먹을 것 같음 안헷갈리니까


★ ★ ★ 증명하고 싶은 가설을 대립가설로 설정됐다 생각하면 됨
귀무가설(H0)
변화,차이 없다 -> group a랑 b는 연관이 없다 -> 두 그룹간의 평균 전환율이 같다 -> 관련성이 없다 -> 유의미한 차이 없다
대립가설(H1)
변화,차이 있다 -> group a랑 b는 연관이 있다 -> 두 그룹간의 평균 전환율은 다르다 -> 관련성이 있다 -> 유의미한 차이 있다
p-value 값 : 귀무가설이 참일 때, 통상 0.05이하이면 귀무가설을 기각하고 대립가설을 채택하는 기준
* 전환율 : 특정한 행위를 한 방문자의 비율
***
- ❓ stats.ttest_ind가 뭔가요?
- 독립표본 t-검정할 때 쓰임, 두 개의 독립된 집단 간 평균의 차이가 통계적으로 유의미한 차이가 있는지를 검정
- 이 함수는 두 집단의 데이터 배열을 입력으로 받아서 t-통계량과 p-값을 반환합니다.
- t-통계량 (statistic)
- 두 그룹 간의 평균 차이가 표준 오차의 몇 배인지를 나타내는 값
- * 표준오차 계산식 scale = sample_std(표준편차) / sqrt(n)
- * n:표본의 크기나 데이터 개수
- 두 집단 간 평균 차이의 크기와 방향(+,-)을 나타냄
- ----> t-통계량이 +이면 a의 평균이 b보다 더 크다는 말임
- p-값 (pvalue)
- p-값은 귀무 가설이 참일 때, 현재 데이터보다 극단적인 결과가 나올 확률입니다.
- 이 값이 유의수준(α) 보다 작으면 귀무 가설을 기각하고 이 값이 유의수준(α) 보다 크면 귀무 가설을 기각하지 않습니다.
- t-통계량 (statistic)
ex)
->
리소스가 부족한 스타트업에서는 몇 퍼센트의 개선에 집착하는 것보다 사용자들이 이미 겪고 있는 불편함이나 개선점에 신경을 쓰는 것이 더 효과적일 수 있다. 따라서 위에서도 언급했지만, 무작정 A/B 테스팅을 하기보다는 좋은 가설을 세우고 A/B 테스팅의 파급력을 고려하여 진행하길 추천한다.
거래 후기 실험을 통해 따뜻한 거래 경험 만들기. 거래 후기 실험을 통해 당근마켓이 어떻게 따뜻한 서비스를 만들고… | by Yedaeun | 당근 테크 블로그 | Medium
3.2 가설검정 # 데이터가 특정 가설을 지지하는지 검정하는게 포인트!


가설검정
- 표본 데이터를 통해 모집단의 가설을 검증하는 과정
- 즉, 데이터가 특정 가설을 지지하는지 평가하는 과정
- 귀무가설(H0)과 대립가설(H1)을 설정하고, 귀무가설을 기각할지를 결정
- 데이터 분석시 두가지 전략을 취할 수 있음
- 확증적 자료분석
- 미리 가설들을 먼저 세운 다음 가설을 검증해 나가는 분석
- 탐색적 자료분석(EDA)
- 가설을 먼저 정하지 않고 데이터를 탐색해보면서 가설 후보들을 찾고 데이터의 특징을 찾는 것
- 확증적 자료분석
☑️ 단계
- 귀무가설(H0)과 대립가설(H1) 설정
- 유의수준(α) 결정
- 검정통계량 계산
- p-값과 유의수준 비교
- 결론 도출
2) 통계적 유의성과 p값
통계적 유의성
- 통계적 유의성은 결과가 우연히 발생한 것이 아니라 어떤 효과가 실제로 존재함을 나타내는 지표
- p값은 귀무 가설이 참일 경우 관찰된 통계치가 나올 확률을 의미
- 일반적으로 p값이 0.05 미만이면 결과를 통계적으로 유의하다고 판단
☑️ p-값
- 귀무가설이 참일 때, 관찰된 결과 이상으로 극단적인 결과가 나올 확률
- 일반적으로 p-값이 유의수준(α)보다 작으면 귀무가설을 기각
- 유의수준으로 많이 사용하는 값이 0.05
☑️ p-값을 통한 유의성 확인
- p-값이 0.03이라면, 3%의 확률로 우연히 이러한 결과가 나올 수 있음
- 일반적으로 0.05 이하라면 유의성이 있다고 봄
3) 신뢰구간과 가설검정의 관계
신뢰구간과 가설검정
- 신뢰구간과 가설검정은 밀접하게 관련된 개념
- 둘 다 데이터의 모수(ex. 평균)에 대한 정보를 구하고자 하는 것이지만 접근 방식이 다름
- 신뢰구간
- 특정 모수가 포함될 범위를 제공
- ❓여기서 잠깐! 신뢰구간이 무엇일까요~?
- 신뢰구간은 모집단의 평균이 특정 범위 내에 있을 것이라는 확률을 나타냅니다.
- 일반적으로 95% 신뢰구간이 사용되며, 이는 모집단 평균이 95% 확률로 이 구간 내에 있음을 의미합니다.
- 만약 어떤 설문조사에서 평균 만족도가 75점이고, 신뢰구간이 70점에서 80점이라면, 우리는 95% 확률로 실제 평균 만족도가 이 범위 내에 있다고 말할 수 있습니다.
- 신뢰구간 (Confidence Interval)
- 가설검정
- 모수가 특정 값과 같은지 다른지 테스트
4) 가설검정이 실제로 어떻게 적용되어질까?
가설을 설정하여 검증
- 새로운 약물이 기존 약물보다 효과가 있는지 검정
- 이 때 새로운 약물은 기존 약물과 큰 차이가 없다는 것이 귀무가설!
- 대립가설은 새로운 약물이 기존 약물과 대비해 교과가 있다는 것!
# 기존 약물(A)와 새로운 약물(B) 효과 데이터 생성
A = np.random.normal(50, 10, 100)
B = np.random.normal(55, 10, 100)
# 평균 효과 계산
mean_A = np.mean(A)
mean_B = np.mean(B)
# t-검정 수행
t_stat, p_value = stats.ttest_ind(A, B)
print(f"A 평균 효과: {mean_A}")
print(f"B 평균 효과: {mean_B}")
print(f"t-검정 통계량: {t_stat}")
print(f"p-값: {p_value}")
# t-검정의 p-값 확인 (위 예시에서 계산된 p-값 사용)
print(f"p-값: {p_value}")
if p_value < 0.05:
print("귀무가설을 기각합니다. 통계적으로 유의미한 차이가 있습니다.")
else:
print("귀무가설을 기각하지 않습니다. 통계적으로 유의미한 차이가 없습니다.")
3.3 t검정 # 가설검정의 대표적인 검정
1) t검정이란 무엇인가?
t검정
- t검정은 두 집단 간의 평균 차이가 통계적으로 유의미한지 확인하는 검정 방법
- 독립표본 t검정과 대응표본 t검정으로 나뉨
☑️ 독립표본 t검정
- 두 독립된 그룹의 평균을 비교
☑️ 대응표본 t검정
- 동일한 그룹의 사전/사후 평균을 비교
2) 가설검정이 실제로 어떻게 적용되어질까?
p-값을 통한 유의성 확인
- 두 클래스의 시험 성적 비교(독립표본 t검정)
- 다이어트 전후 체중 비교(대응표본 t검정)
# 학생 점수 데이터
scores_method1 = np.random.normal(70, 10, 30)
scores_method2 = np.random.normal(75, 10, 30)
# 독립표본 t검정
t_stat, p_val = stats.ttest_ind(scores_method1, scores_method2)
print(f"T-Statistic: {t_stat}, P-value: {p_val}")
3.4 다중검정 # 여러 가설을 동시에 검정! 하지만 오류가 발생할 수 있음!
1) 다중검정이란 무엇인가?
다중검정
- 여러 가설을 동시에 검정할 때 발생하는 문제
- 각 검정마다 유의수준을 조정하지 않으면 1종 오류(귀무가설이 참인데 기각하는 오류) 발생 확률이 증가
- 1종 오류가 무엇인지랑 왜 다중검정시 발생확률이 증가하는지는 밑에서 다시 설명! 지금은, 어떤 오류가 발생할 수 있다는 정도로 이해!
☑️ 보정 방법
- 본페로니 보정, 튜키 보정, 던넷 보정, 윌리엄스 보정 등이 있음
- 가장 대표적이고 기본적인게 본페로니 보정
2) 다중검정과 보정을 어떻게 적용되어질까?
여러 약물의 효과를 동시에 검정
- 이 때 본페로니 보정을 사용해볼 수 있음
import numpy as np
import scipy.stats as stats
# 세 그룹의 데이터 생성
np.random.seed(42)
group_A = np.random.normal(10, 2, 30)
group_B = np.random.normal(12, 2, 30)
group_C = np.random.normal(11, 2, 30)
# 세 그룹 간 평균 차이에 대한 t검정 수행
p_values = []
p_values.append(stats.ttest_ind(group_A, group_B).pvalue)
p_values.append(stats.ttest_ind(group_A, group_C).pvalue)
p_values.append(stats.ttest_ind(group_B, group_C).pvalue)
# 본페로니 보정 적용
alpha = 0.05
adjusted_alpha = alpha / len(p_values)
# 결과 출력
print(f"본페로니 보정된 유의 수준: {adjusted_alpha:.4f}")
for i, p in enumerate(p_values):
if p < adjusted_alpha:
print(f"검정 {i+1}: 유의미한 차이 발견 (p = {p:.4f})")
else:
print(f"검정 {i+1}: 유의미한 차이 없음 (p = {p:.4f})")
3.5 카이제곱검정 # 범주형 데이터의 분석에 사용한다는 것이 포인트!
1) 카이제곱검정이란 무엇인가?
카이제곱검정
- 범주형 데이터의 표본 분포가 모집단 분포와 일치하는지 검정(적합도 검정)하거나
- 두 범주형 변수 간의 독립성을 검정(독립성 검정)
☑️ 적합도 검정
- 관찰된 분포와 기대된 분포가 일치하는지 검정
- p값이 높으면 데이터가 귀무 가설에 잘 맞음. 즉, 관찰된 데이터와 귀무 가설이 적합
- p값이 낮으면 데이터가 귀무 가설에 잘 맞지 않음. 즉, 관찰된 데이터와 귀무 가설이 부적합
☑️ 독립성 검정
- 두 범주형 변수 간의 독립성을 검정
- p값이 높으면 두 변수 간의 관계가 연관성이 없음 → 독립성이 있음
- p값이 낮으면 두 변수 간의 관계가 연관성이 있음 → 독립성이 없음
2) 카이제곱검정은 어떻게 적용되어질까?
범주형 데이터의 분포 확인 및 독립성 확인을 위해 사용
- 주사위의 각 면이 동일한 확률로 나오는지 검정(적합도 검정)
- 성별과 직업 만족도 간의 독립성 검정(독립성 검정)
# 적합도 검정
observed = [20, 30, 25, 25]
expected = [25, 25, 25, 25]
chi2_stat, p_value = stats.chisquare(observed, f_exp=expected)
print(f"적합도 검정 카이제곱 통계량: {chi2_stat}, p-값: {p_value}")
# 독립성 검정
observed = np.array([[10, 10, 20], [20, 20, 40]])
chi2_stat, p_value, dof, expected = stats.chi2_contingency(observed)
print(f"독립성 검정 카이제곱 통계량: {chi2_stat}, p-값: {p_value}")
# 나이와 흡연 여부 독립성 검정
observed = np.array([[30, 10], [20, 40]])
chi2_stat, p_value, dof, expected = stats.chi2_contingency(observed)
print(f"독립성 검정 카이제곱 통계량: {chi2_stat}, p-값: {p_value}")
********************************************여기까지 이해함 1.17기준 ******************************************************
- ❓ stats.chisquare 함수가 뭔가요?
- scipy.stats.chisquare 함수는 카이제곱 적합도 검정을 수행하여 관찰된 빈도 분포가 기대된 빈도 분포와 일치하는지 평가합니다. 이 검정은 주로 단일 표본에 대해 관찰된 빈도가 특정 이론적 분포(예: 균등 분포)와 일치하는지 확인하는 데 사용됩니다.
- 반환 값
- chi2: 카이제곱 통계량입니다.
- p: p-값입니다. 이는 관찰된 데이터가 귀무 가설 하에서 발생할 확률입니다.
**
- ❓ stats.chi2_contingency 함수가 뭔가요?
- scipy.stats.chi2_contingency 함수는 카이제곱 검정을 수행하여 두 개 이상의 범주형 변수 간의 독립성을 검정합니다. 이 함수는 관측 빈도를 담고 있는 교차표(contingency table)를 입력으로 받아 카이제곱 통계량, p-값, 자유도, 그리고 기대 빈도(expected frequencies)를 반환합니다.
- 반환 값
- chi2 : 카이제곱 통계량입니다.
- p : p-값입니다. 이는 관측된 데이터가 귀무 가설 하에서 발생할 확률입니다.
- dof : 자유도입니다. 이는 (행의 수 - 1) * (열의 수 - 1)로 계산됩니다.
- expected : 기대 빈도입니다. 이는 행 합계와 열 합계를 사용하여 계산된 이론적 빈도입니다.
3.6 제 1종 오류와 제 2종 오류 #두가지의 오류를 구분하는 것이 포인트!

제 1종 오류
- 귀무가설이 참인데 기각하는 오류
- 잘못된 긍정을 의미 (아무런 영향이 없는데 영향이 있다고 하는 것)
- 한 단어로 위양성!
- α(알파)를 경계로 귀무가설을 기각하기 때문에 제1종 오류가 α만큼 발생
- 따라서 유의수준(α)을 정함으로써 제 1종 오류 제어 가능
- 만약, 유의수준이 0.05라면 100번 중 5번 정도 일어날 수 있는 제 1종 오류는 감수하겠다는 것
- ❓다중 검정시 제 1종 오류가 증가하는 이유?
- 하나의 검정에서 제1종 오류가 발생하지 않을 확률은 1- α 입니다.
- m개의 독립된 검정에서 제1종 오류가 전혀 발생하지 않을 확률은 (1- α )^m입니다.
- 따라서, m개의 검정에서 하나 이상의 제1종 오류가 발생할 확률(즉, 전체 제1종 오류율)은 1-(1- α )^m입니다.
- 이 값은 m이 커질수록 빠르게 증가합니다. 예를 들어, α=0.05, m=10인 경우
- 1 - (1 - 0.05)^10 는 0.401와 유사하다
- 즉, 10개의 가설을 동시에 검정할 때 하나 이상의 가설에서 제 1종 오류가 발생할 확률이 약 40.1% 이므로 개별검증에서 발생하는 오류율(5%)보다 높습니다.
제 2종 오류
- 귀무가설이 거짓인데 기각하지 않는 오류.
- 잘못된 부정을 의미 (영향이 있는데 영향이 없다고 하는 것)
- 한 단어로 위음성!
- 제 2종 오류가 일어날 확률은 β로 정의.
- 제 2종 오류가 일어나지 않을 확률은 검정력(1-β)으로 정의.
- 하지만 이를 직접 통제할 수는 없음.
- 그나마 통제를 해볼 수 있는 방법으로는…
- 표본크기 n이 커질 수록 β가 작아짐.
- α와 β는 상충관계에 있어서 너무 낮은 α를 가지게 되면 β는 더욱 높아짐
☑️ 예시
- 새로운 약물이 효과가 없는데 있다고 결론 내리는 것(제 1종 오류).
- 효과가 있는데 없다고 결론 내리는 것(제 2종 오류).
** np.random.binomial (이항분포), np.random.normal (정규분포) 의 차이
(공통점)
둘 다 두 가지 다른 확률 분포에서 난수를 생성하는 함수임
(차이점)
생성되는 데이터의 분포와 특성이 다름
np.random.binomial (n: 한번의 실험당 시행 횟수, p: 성공 확률, size: 실험 횟수)
-> 성/실 두 가지 가능한 결과가 있는 실험에서 쓰임
np.random.normal (loc: 정규 분포의 평균, scale: 분포의 표준편차, size: 생성할 샘플의 개수)
-> 연속적인 값을 가지며, 대부분의 값들이 평균값 근처에 모여 있는 분포임(=가우시안 분포)
주로 평균과 표준편차를 기반으로 함
3.7 연습문제
1.가설검정에서 사용되는 주요 개념 중 하나인 p-value의 의미를 설명하세요.
- p-value는 두 그룹 간의 평균 차이를 나타낸다.
- p-value는 귀무가설이 참일 때, 관찰된 데이터 또는 더 극단적인 데이터가 나타날 확률이다.
- p-value는 두 그룹 간의 표준편차를 나타낸다.
- p-value는 실험 그룹의 크기를 나타낸다.
2번(정답)
2. 가설검정에서 귀무가설(null hypothesis)과 대립가설(alternative hypothesis)의 차이에 대한 설명으로 옳은 것을 고르세요.
- 귀무가설은 연구자가 입증하고자 하는 주장이고, 대립가설은 현재 상태를 나타낸다.
- 귀무가설은 현재 상태를 나타내며, 대립가설은 연구자가 입증하고자 하는 주장이다.
- 귀무가설과 대립가설은 동일한 개념이다.
- 귀무가설은 대립가설의 반대를 나타낸다.
4번(오답 2번이 정답)
해설:
가설검정에서 귀무가설은 연구자가 입증하는 주장과는 아무 상관없는 현재 상태나 기존의 믿음을 나타내며, 대립가설은 연구자가 입증하고자 하는 새로운 주장입니다.
gpt해설 :
"귀무가설은 대립가설의 반대를 나타낸다"는 설명은 귀무가설이 대립가설과 상반된 주장이라고 간단히 정의할 수 있지만, 두 가설 간의 관계를 너무 간단하게 이해한 것입니다. 실제로는 귀무가설과 대립가설은 상호 보완적인 관계에 있으며, 귀무가설이 부정될 때 대립가설을 채택하는 구조입니다.
3. 두 그룹의 평균이 서로 다른지 비교하기 위해 사용되는 t검정의 종류는 무엇인가요?
- 독립 표본 t검정
- 대응 표본 t검정
- 분산 분석
- 카이제곱검정
1번(정답)
4. 다중검정에서 발생할 수 있는 문제점은 무엇인가요?
- 표본의 크기가 작아진다.
- 한 번의 검정에서 제 1종 오류가 발생할 확률이 감소한다.
- 여러 번의 검정을 수행할 때, 전체 실험에서 제 1종 오류가 발생할 확률이 증가한다.
- 한 번의 검정에서 제 2종 오류가 발생할 확률이 증가한다.
3번(정답)
5. 카이제곱검정은 주로 어떤 데이터를 분석할 때 사용되나요?
- 연속형 데이터
- 범주형 데이터
- 비율 데이터
- 순서형 데이터
2번(정답)
6. 제 1종 오류(Type I error)와 제 2종 오류(Type II error)의 차이에 대한 설명으로 옳은 것을 고르세요.
- 제 1종 오류는 귀무가설이 참인데 기각하는 오류이고, 제 2종 오류는 대립가설이 참인데 기각하는 오류이다.
- 제 1종 오류는 대립가설이 참인데 기각하는 오류이고, 제 2종 오류는 귀무가설이 참인데 기각하는 오류이다.
- 제 1종 오류와 제 2종 오류는 동일한 개념이다.
- 제 1종 오류는 표본 크기와 관련이 없고, 제 2종 오류는 표본 크기와 관련이 있다.
1번(정답)
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
4주차 회귀(Regression)
** r spr 값 = 결정계수 = 정확도라 이해해도 좋음
[수업 목표]
★ 회귀가 무엇인지에 대해 이해한다
현재의 데이터를 바탕으로 미래를 예측할 때 회귀(Regression)이 쓰임
근데, 회귀라는 것이 결국 미래 예측값보다 튀거나 가라앉을 수 있는데 결국은 결향성에 맞춰진다는 내용
★ 다양한 회귀의 종류에 대해서 설명할 수 있고 특징을 이해한다
단순선형회귀: 하나의 독립 변수(X)와 하나의 종속 변수(Y) 간의 관계를 직선으로 모델링하는 방법
다중선형회귀: 두 개 이상의 독립 변수(X1, X2, ..., Xn)와 하나의 종속 변수(Y) 간의 관계를 모델링
다항회귀
- 독립 변수와 종속 변수 간의 관계가 선형이 아닐 때 사용. 독립 변수의 다항식을 사용하여 종속 변수를 예측.
- 데이터가 곡선적 경향을 따를 때 사용합니다.
- 비선형 관계를 모델링할 수 있습니다.
- 고차 다항식의 경우 과적합(overfitting) 위험이 있습니다.
스플라인 회귀
- 독립 변수의 구간별로 다른 회귀식을 적용하여 복잡한 관계를 모델링
- 구간마다 다른 다항식을 사용하여 전체적으로 매끄러운 곡선을 생성합니다.
- 데이터가 국부적으로 다른 패턴을 보일 때 사용합니다.
- 복잡한 비선형 관계를 유연하게 모델링할 수 있습니다.
- 적절한 매듭점(knots)의 선택이 중요합니다.
4.1 단순선형회귀 # 한개의 변수에 의한 결과를 예측
단순선형회귀란 무엇인가?
단순선형회귀
- 하나의 독립 변수(X)와 하나의 종속 변수(Y) 간의 관계를 직선으로 모델링하는 방법.
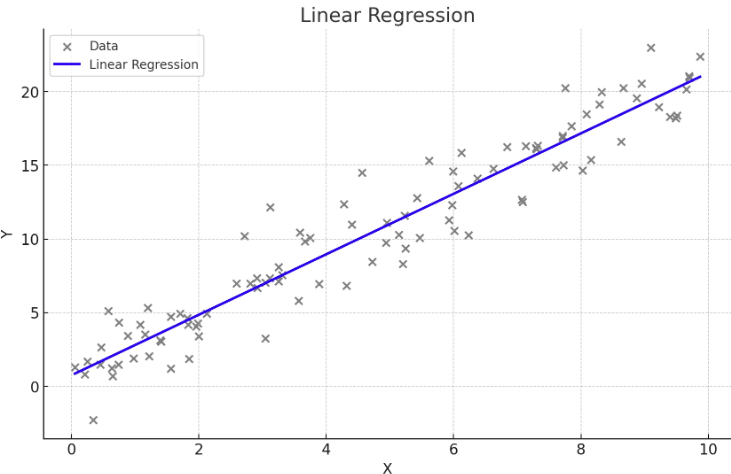
회귀식
- Y = β0 + β1X, 여기서 β0는 절편, β1는 기울기
- ex) y = ax + b 에서 ax는 기울기이고 b는 절편임, 절편 맛있음
☑️ 특징
- 독립 변수의 변화에 따라 종속 변수가 어떻게 변화하는지 설명하고 예측.
- 데이터가 직선적 경향을 따를 때 사용합니다.
- 간단하고 해석이 용이합니다.
- 데이터가 선형적이지 않을 경우 적합하지 않습니다.
단순선형회귀는 어떨 때 사용할까?
하나의 독립변수와 종속변수와의 관계를 분석 및 예측
- 광고비(X)와 매출(Y) 간의 관계 분석.
- 현재의 광고비를 바탕으로 예상되는 매출을 예측 가능.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression #마신라닝에서 배우는 라이브러리니 참고만 하자1
from sklearn.model_selection import train_test_split #마신라닝에서 배우는 라이브러리니 참고만 하자2
from sklearn.metrics import mean_squared_error, r2_score # 마신라닝에서 배우는 라이브러리니 참고만 하자3
# 예시 데이터 생성
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 단순선형회귀 모델 생성 및 훈련
model = LinearRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 회귀 계수 및 절편 출력
print("회귀 계수:", model.coef_)
print("절편:", model.intercept_)
# 모델 평가
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)
# 시각화
plt.scatter(X, y, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=2)
plt.title('linear regeression')
plt.xlabel('X : cost')
plt.ylabel('Y : sales')
plt.show()
4.2 다중선형회귀 # 두 개 이상의 변수에 의한 결과를 예측
다중선형회귀란 무엇인가?
다중선형회귀
- 두 개 이상의 독립 변수(X1, X2, ..., Xn)와 하나의 종속 변수(Y) 간의 관계를 모델링.

회귀식
- Y = β0 + β1X1 + β2X2 + ... + βnXn
☑️ 특징
- 여러 독립 변수의 변화를 고려하여 종속 변수를 설명하고 예측
- 종속변수에 영향을 미치는 여러 독립변수가 있을 때 사용합니다.
- 여러 변수의 영향을 동시에 분석할 수 있습니다.
- 변수들 간의 다중공선성 문제가 발생할 수 있습니다.
- ❓ 다중공선성이 무엇인가요~?
- 다중공선성(Multicollinearity)은 회귀분석에서 독립 변수들 간에 높은 상관관계가 있는 경우를 말합니다.
- 이는 회귀분석 모델의 성능과 해석에 여러 가지 문제를 일으킬 수 있습니다.
- 독립 변수들이 서로 강하게 상관되어 있으면, 각 변수의 개별적인 효과를 분리해내기 어려워져 회귀의 해석을 어렵게 만듭니다.
- 다중공선성으로 인해 실제로 중요한 변수가 통계적으로 유의하지 않게 나타날 수 있습니다.
- 어떻게 진단할 수 있을까요~?
- 가장 간단한 방법으로는 상관계수를 계산하여 상관계수가 높은(약 0.7) 변수들이 있는지 확인해볼 수 있습니다.
- 더 정확한 방법으로는 분산 팽창 계수 (VIF)를 계산하여 VIF값이 10이 높은지 확인하는 방법으로 다중공선성이 높다고 판단할 수 있습니다.
- 다중공선성 해결 방법
- 가장 간단한 방법으로는 높은 계수를 가진 변수 중 하나를 제거하는 것입니다.
- 혹은 주성분 분석(PCA)과 같은 변수들을 효과적으로 줄이는 차원 분석 방법을 적용하여 해결할 수도 있습니다.
- 다중선형회귀는 어떨 때 사용할까?
- 다양한 광고비(TV, Radio, Newspaper)과 매출 간의 관계 분석.
- 현재의 광고비(TV, Radio, Newspaper)를 바탕으로 예상되는 매출을 예측 가능.
- ☑️ 두 개 이상의 독립 변수와 종속변수와의 관계를 분석 및 예측
# 예시 데이터 생성
# np.random.rand(100) : 0과 1사이의 난수 100개를 무작위로 생성한 배열을 반환
data = {'TV': np.random.rand(100) * 100,
'Radio': np.random.rand(100) * 50,
'Newspaper': np.random.rand(100) * 30,
'Sales': np.random.rand(100) * 100}
df = pd.DataFrame(data)
# 독립 변수(X)와 종속 변수(Y) 설정
# df[['TV', 'Radio', 'Newspaper']] : 'TV', 'Radio', 'Newspaper' 세 개의 열만 포함된 새로운 DataFrame을 반환함
# df['TV', 'Radio', 'Newspaper'] 는 잘못된 구문임.
# 열 선택하는데 여러 열을 동시에 선택하려고 할 때는 튜플 형태로 처리되서 튜플을 인덱싱 하는 꼴이 됨
# DateFrame에서 튜플은 지원을 안함 즉, 오류남
X = df[['TV', 'Radio', 'Newspaper']]
y = df['Sales']
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 다중선형회귀 모델 생성 및 훈련
model = LinearRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 회귀 계수 및 절편 출력
print("회귀 계수:", model.coef_)
print("절편:", model.intercept_)
# 모델 평가
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)
4.3 범주형 변수 # 회귀에서 범주형 변수의 경우 특별히 변환을 해주어야 함!
회귀에서의 범주형 변수
범주형 변수
- 수치형 데이터가 아닌 주로 문자형 데이터로 이루어져 있는 변수가 범주형 변수
☑️ 범주형 변수 종류
- 예를 들어 성별(남, 여), 지역(도시, 시골) 등이 있으며, 더미 변수로 변환하여 회귀 분석에 사용.
- 순서가 있는 범주형 변수
- 옷의 사이즈 (L, M, …), 수능 등급 (1등급, 2등급, ….)과 같이 범주형 변수라도 순서가 있는 변수에 해당한다
- 이런 경우 각 문자를 임의의 숫자로 변환해도 문제가 없다 (순서가 잘 반영될 수 있게 숫자로 변환)
- ex) XL → 3, L → 2, M → 1, S → 0
- 순서가 없는 범주형 변수
- 성별 (남,여), 지역 (부산, 대구, 대전, …) 과 같이 순서가 없는 변수에 해당한다
- 2개 밖에 없는 경우 임의의 숫자로 바로 변환해도 문제가 없지만
- 3개 이상인 경우에는 무조건 원-핫 인코딩(하나만 1이고 나머지는 0인 벡터)변환을 해주어야 한다 → pandas의 get_dummies를 활용하여 쉽게 구현 가능
- ex) 부산 = [1,0,0,0], 대전 = [0,1,0,0], 대구 = [0,0,1,0], 광주 = [0,0,0,1]
- 순서가 있는 범주형 변수
범주형 변수는 어떻게 사용할까?
범주형 변수를 찾고 더미 변수로 변환한 후 회귀 분석 수행
- 성별, 근무 경력과 연봉 간의 관계.
- 성별과 근무 경력이라는 요인변수 중 성별이 범주형 요인변수에 해당
- 해당 변수를 더미 변수로 변환
- 회귀 수행
# 예시 데이터 생성
data = {'Gender': ['Male', 'Female', 'Female', 'Male', 'Male'],
'Experience': [5, 7, 10, 3, 8],
'Salary': [50, 60, 65, 40, 55]}
df = pd.DataFrame(data)
# 범주형 변수 더미 변수로 변환
df = pd.get_dummies(df, drop_first=True)
# 독립 변수(X)와 종속 변수(Y) 설정
X = df[['Experience', 'Gender_Male']]
y = df['Salary']
# 단순선형회귀 모델 생성 및 훈련
model = LinearRegression()
model.fit(X, y)
# 예측
y_pred = model.predict(X)
# 회귀 계수 및 절편 출력
print("회귀 계수:", model.coef_)
print("절편:", model.intercept_)
# 모델 평가
mse = mean_squared_error(y, y_pred)
r2 = r2_score(y, y_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)
4.4 다항회귀, 스플라인 회귀 # 데이터가 훨씬 복잡할 때 사용하는 회귀!
다항회귀, 스플라인 회귀란 무엇인가?
☑️ 다항회귀
- 독립 변수와 종속 변수 간의 관계가 선형이 아닐 때 사용. 독립 변수의 다항식을 사용하여 종속 변수를 예측.
- 데이터가 곡선적 경향을 따를 때 사용합니다.
- 비선형 관계를 모델링할 수 있습니다.
- 고차 다항식의 경우 과적합(overfitting) 위험이 있습니다.

☑️ 스플라인 회귀
- 독립 변수의 구간별로 다른 회귀식을 적용하여 복잡한 관계를 모델링
- 구간마다 다른 다항식을 사용하여 전체적으로 매끄러운 곡선을 생성합니다.
- 데이터가 국부적으로 다른 패턴을 보일 때 사용합니다.
- 복잡한 비선형 관계를 유연하게 모델링할 수 있습니다.
- 적절한 매듭점(knots)의 선택이 중요합니다.

다항회귀는 어떨 때 사용할까?
☑️ 독립변수와 종속변수의 관계가 비선형 관계일 때 사용
- 주택 가격 예측(면적과 가격 간의 비선형 관계)
from sklearn.preprocessing import PolynomialFeatures
# 예시 데이터 생성
np.random.seed(0)
X = 2 - 3 * np.random.normal(0, 1, 100)
y = X - 2 * (X ** 2) + np.random.normal(-3, 3, 100)
X = X[:, np.newaxis]
# 다항 회귀 (2차)
polynomial_features = PolynomialFeatures(degree=2)
X_poly = polynomial_features.fit_transform(X)
model = LinearRegression()
model.fit(X_poly, y)
y_poly_pred = model.predict(X_poly)
# 모델 평가
mse = mean_squared_error(y, y_poly_pred)
r2 = r2_score(y, y_poly_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)
# 시각화
plt.scatter(X, y, s=10)
# 정렬된 X 값에 따른 y 값 예측
sorted_zip = sorted(zip(X, y_poly_pred))
X, y_poly_pred = zip(*sorted_zip)
plt.plot(X, y_poly_pred, color='m')
plt.title('polynomial regerssion')
plt.xlabel('area')
plt.ylabel('price')
plt.show()
4.5 연습문제




ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
코드카타

오답 1. 들여쓰기 문제인거 같다 근데 모르겠어 ..
def solution(num):
count = 0
while count < 500:
if num % 2 == 0:
num = num/2
count += 1
# elif num % 3 == 0: 는 잘못된 조건문임 짝수와 홀수일 때 연산이 각각 정의되어 있기 때문에 elif로 구분할 필요 없음
# 제안 : 오히려 짝수일땐 if로 쓰고 홀수일땐 자연스레 else가 되게끔
elif num % 3 == 0:
num = (num*3)+1
count += 1
# elif num % 3 == 0: 에서 num 이 1 되는 경우를 확인하고 break로 종료하는데, num == 1은 그 전 while문을 중단하는 방식임. 만약 num이 1이 되면 count를 출력하고 즉시 종료하므로, 만약 500번 작업이 지나지 않았어도 종료되는 점에서 코드 흐름이 의도와 다를 수 있습니다.
# 제안1 : num ==1 일때는 바로 count 출력하고 종료하도록 return 사용
# 제안 2 : while count < 500: 조건을 넘기기 전에 num == 1이면 그 즉시 출력하고 종료하는 로직을 명확히 해야 합니다.
if num == 1:
print(count)
break
solution(12)
오답 2. 애초에 break 문을 제일 먼저 걸어놨어야함 , 그다음에 들어갈 if를 그냥 이어서 써야했네?
어렵다 .. .젠장 ㅠㅠㅠ 근데 왜 통과를 못할까?
| 실행 결과 〉 | 실행한 결괏값 null이 기댓값 8과 다릅니다. |
왜??????????????????????????????????????????
print는 단순히 값을 보여주는 것임. 단순 카운트 띄우기 용
return 은 그 값을 함수 밖으로 돌려주는 것. 카운트 띄우기 + 띄운 카운트를 다른 곳에서 사용할 수 있게 버무려주기
그니까 print 쓰지말고 return으로 비스므리하게 바꿔줘야했음
난 이해가 아직 안됐거든? 좀 더 봐야겠어
위 함수를 그대로 써서 다른 함수랑 연계가 되는지 확인하면 되는거잖아?
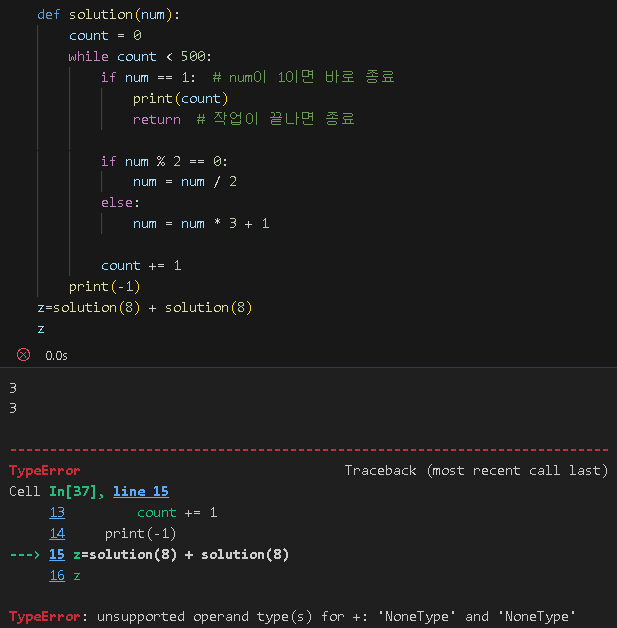
논 타입이라 안된다네
밑에 정답 코드로 작업하면 z값 6 잘나옴 ㅇㅇ .. ㅇㅋ
** None : NomeType 형의 유일한 값. None은 기본 인자가 함수에 전달되지 않을 때처럼, 값의 부재를 나타내는 데 자주 사용됩니다. None은 대입할 수 없고 SyntaxError를 일으킵니다.
정답.
다른 사람 풀이
def collatz(num):
for i in range(500):
num=num/2 if num%2==0 else num*3+1
if num==1:
return i+1
return -11. for 문에 range(500) 쓰면 이후에 문제 있을까봐 안썼는데 아니네?
2. 근데 이해가 안되네?
본인 해석 :
i가 1~499까지 반복할거야.. 만약 num값이 짝수면 2나누고 나머지면 3곱해서 1더해
만약 num값이 1이면 i값에다가 1을 더해서 결과값을 출력해
결과값 출력을 못했으면 그냥 -1로 출력해
Q1. ==>> 음 그럼 collatz(8) 이면 3이 출력되는건데 8 -> 4 -> 2 -> 1 이여서 3+1 이니까 4가 나오는거 아냐? 왜 3 나오지?
아 ... 순서가 조금 다르네 먼저 나누고 나중에 더해주네 ? 근데 그럼 i는 어떤 개념으로 쓰인거야 !!!!
Q2. ==>> for문은 반복의 개념으로도 쓰이는데 i값이 하단에 아무것도 없는데 어떤 의미로 쓰인건지??
A.
for i in range(10):
print("ㅗ")
를 쓰면 i가 없어도 알아서 굴러가잖아? 출력이 ㅗ ㅗ ㅗ ㅗ ㅗ.... 9번 나오잖아?
현재 for i in range(500): 도 결국 함수 내에서 499번 굴러간다는 뜻이지 굳이 i 가 들어갈 필요는 없음
-> 개념 이해가 부족했다~
'본 캠프 TIL' 카테고리의 다른 글
| 1월 21일 TIL 통계학 라이브 세션 4차, 코드카타 (2) | 2025.01.21 |
|---|---|
| 1월 20일 TIL 통계학 라이브 세션 3회차, 5,6주차, 마쉰라닝 기초 겉핥기, 코드카타, 아티클 (0) | 2025.01.20 |
| 1월16일 TIL 라이브 세션, 통계학 1&2주차, 코드카타, 아티클 스터디 (0) | 2025.01.16 |
| 1월 14일 TIL (팀 프로젝트 발표) (1) | 2025.01.14 |
| 1월13일 TIL (팀프로젝트 준비) (0) | 2025.01.13 |