통계학 라이브 세션 4차 정강민 튜터님
오늘의 요약
- 카이제곱 검정
- 적합성 검정: 단일 범주의 “관찰분포 vs 이론(기대)분포” 비교
- 독립성 검정: 하나의 모집단 내 두 범주형 변수의 독립성 판단
- 동질성 검정: 여러 모집단에서 하나의 범주형 변수의 분포가 같은지 비교
- 선형회귀
- 종속변수가 연속형일 때, 독립변수들과의 관계를 추정
- 단순(1개 독립변수) vs 다중(여러 독립변수)
- ANOVA(분산분석)
- 범주형 독립변수(집단)에 따른 연속형 종속변수(평균차이) 분석
- 일원(1개 요인) vs 이원(2개 요인, 상호작용 포함)
- 로지스틱 회귀
- 종속변수가 범주형(이진 또는 다항)일 때 사용
- 이진 로지스틱(0/1) vs 다항 로지스틱(3개 이상의 범주)
*
데이터 입력값
x y
범주 범주 : 카이 제곱 검정 (*그리스어로 X가 카이임)
범주 수치 : 아노바, t검정
수치 범주 : 로지스틱(수치를 받아 불린 형태로 아웃풋함)
수치 수치 : 선형 회귀 - 통계에서의 선형 회귀와 머신러닝에서의 선형 회귀가 약간 다름
**
어느 제과점에서 효모 A, B, C를 사용해 빵을 구웠을 때의 “팽창률”이 서로 차이가 나는지 확인하고 싶다.
-> 범주 a,b,c/수치 팽찰률
=> 아노바 분석 사용
(t검정은 변수가 2개 일 때 사용, 카이제곱 검정은 데이터 형식이 범주형일 때 사용)
***
스타트업에서 직원들의 생산성 점수(예: 단위시간당 처리 업무량)를 예측하기 위해,
“주당 근무시간, 재택근무 여부(더미 변수로 변환), 직무만족도, 팀 내 커뮤니케이션 점수” 등을 예측 변수로 사용하는 모델을 개발하려 한다.
-> 수치 생산성 점수 / 수치 시간 등
=> 선형회귀 (다중 선형회귀 사용)
****
인터넷 쇼핑 몰에서 구매완료, 장바구니에 보유하고 있을지
-> o.x 불린 타입
=> 로지스틱 사용
[수업 목표]
- 카이제곱 검정을 통해 범주형 변수 간 독립성에 대한 가설 검정과 p-value 해석 방법을 익힌다.
- 독립성 검정, 적합도 검정, 동질성 검정 등 다양한 카이제곱 검정 방법을 이해한다.
- Python의 scipy.stats를 활용하여 카이제곱 통계량과 p-value를 계산하고, Cramer's V를 활용한 연관성 강도 측정 방법을 이해한다.(Cramer's V : 두 변수가 얼마나 강력하게 결합되어 있나 확인할 때 사용, 명확한 기준 있음)
- 제조 품질 데이터를 활용하여 생산라인과 불량률의 연관성, 개선 전후 품질 변화 등을 통계적으로 분석하는 방법을 이해한다.
1. 카이제곱 (χ2) 분석 개요
(1) 기본 개념
카이제곱 검정 (Chi-square test) 은 📊 범주형 자료 간의 관계나 분포 적합도를 검정하는 데 사용되는 통계 기법입니다.
(2) 범주형 자료 예시 (보통 str 타입)
- 성별 (남/여), 혈액형 (A/B/O/AB), 지역 (서울/경기/인천/...),
- 제품 만족도 (매우 만족/만족/보통/불만족/매우 불만족) 등 -> {매우 만족:5, 만족:4 ...} 이런 식이여도 범주형임
- ex)타이타닉 생존율은 0과 1로 나눠져 있음 -> 범주형으로 봐야함
- 즉 전처리를 잘해줘야함
(3) 데이터에서 교차표로 변환
데이터 → 교차표 변환
1. 데이터 예시: 일반 레이블 형태
한 제조업체에서 생산 라인(A, B, C)과 제품 상태(양품/불량) 데이터를 수집했다고 가정합니다.

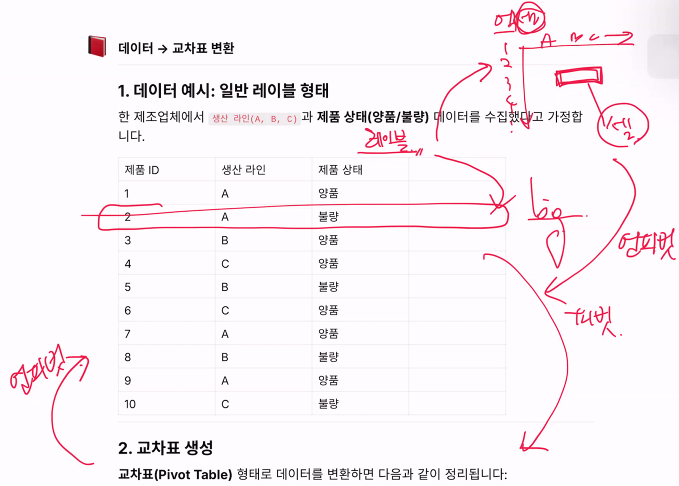
2. 교차표 생성
교차표(Pivot Table) 형태로 데이터를 변환하면 다음과 같이 정리됩니다: # 자유도 (3-1)(2-1) = 2

해당 범주의 빈도를 나타냅니다.
3. Python Code로 변환 예시
import pandas as pd
# 1. 데이터 생성
data = {
"제품 ID": [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
"생산 라인": ["A", "A", "B", "C", "B", "C", "A", "B", "A", "C"],
"제품 상태": ["양품", "불량", "양품", "양품", "불량", "양품", "양품", "불량", "양품", "불량"],
}
df = pd.DataFrame(data)
# 2. 교차표 생성
cross_tab = pd.crosstab(df["생산 라인"], df["제품 상태"], margins=True, margins_name="합계")
# 3. 출력
print(cross_tab)
4. 출력 결과

2. 카이제곱 검정의 주요 유형
- 적합도 검정(Goodness-of-fit test) 차이가 유의미한지 알아내는 검정
- 하나의 범주형 변수에 대해 ‘이론적으로 기대되는 분포(기댓값)’가 있고, 이것이 실제 관찰된 분포(관측값)와 유의미하게 다른지를 검정합니다.
- 예) “5종류 사탕이 균등하게(각각 20%) 섞여 있다”는 가정과, 실제 뽑힌 사탕 빈도를 비교하는 문제.
- 교차분석(Cross tabulation analysis) : 독립성, 동질성 검정 가능
- 두 개 이상의 범주형 변수가 서로 관련(독립이 아님)되어 있는지 분석합니다.
- 예) “남학생과 여학생”이 “메뉴(짜장면, 짬뽕, 마라탕)”를 선택하는 빈도가 유의하게 다른지 알아보는 문제.
- 이를 독립성 검정(Chi-square test of independence)이라고 부르기도 합니다.
또 다른 갈래, 검정 독립성, 동질성, 적합도
(1) 적합도 (Goodness-of-fit) 검정
- 하나의 범주형 변수가 어떤 특정한 기대 분포 (이론적 분포) 에 적합한지 확인합니다. (p-value 값 사용)
- 예시: 멘델의 유전 법칙에서 예상되는 표현형 비율 (둥근 완두콩 : 주름진 완두콩 = 3:1) 이 실제 관찰 결과와 일치하는지 검정
- 귀무가설 (H0): 관측된 분포 = 기대 분포 (차이 없음)
- 대립가설 (H1): 관측된 분포 =! 기대 분포(차이 있음)
- ex) (유의수준 0.05 기준) p-value 값이 0.05 보다 작으면 귀무가설 기각 / 대립가설 채택 차이 있음
(2) 독립성 (Independence) 검정
- 두 개의 범주형 변수가 서로 독립인지, 아니면 연관성이 있는지 확인합니다.
- 예시: 성별과 특정 질병 발병 여부가 연관되는지 검정
- 귀무가설 (H0): 두 범주형 변수는 서로 독립
(3) 동질성 (Homogeneity) 검정
- 여러 모집단 (집단) 이 동일한 분포를 보이는지 검정합니다.
- 예시: 지역별로 특정 제품에 대한 선호도 분포가 동일한지 검정
- 귀무가설 (H0): 여러 집단 간 범주형 분포는 모두 동일
💡 독립성 검정과 동질성 검정은 통계적으로 유사한 방식으로 진행되지만,
해석상 "서로 다른 모집단들이 동일한 분포를 보이는지" 를 묻는 점이 다릅니다. 💡
- 적합성 검정: chisquare()
- “단일 범주형 변수의 관측분포가 주어진 이론적 분포와 얼마나 잘 맞는가?”
- 독립성 검정: chi2_contingency()
- “하나의 모집단에서 두 범주형 변수가 서로 독립인가?”
- 동질성 검정: chi2_contingency()
- “서로 다른 여러 모집단에서 하나의 범주형 변수의 분포가 동일(동질)한가?”
코드 차원에서는 독립성 검정과 동질성 검정이 똑같이 chi2_contingency를 이용하지만,
어떤 맥락(자료 수집 방식, 행/열의 의미 등)으로 해석하는지가 다릅니다.
3. 수학적 기초
예시
- 자유도 k인 카이제곱 분포는 서로 독립인 k개의 표준정규분포 확률변수 $X_1, X_2, \dots, X_k$의 제곱합에 대한 분포입니다.

- 주로 범주형 자료의 빈도를 다룰 때(적합도 검정, 교차분석 등) 많이 사용됩니다.
적합도 검정 예시
예시 상황
- 5종류의 사탕이 똑같은 비율(각 20%)로 섞여 있다고 가정(총 100개 중 맛별로 20개씩 기대). -> 기대값
- 실제로 뽑은 관찰값(소다맛 17, 딸기맛 16, 레몬맛 24, 포도맛 29, 사과맛 14). -> 관측값

카이제곱 통계량 계산
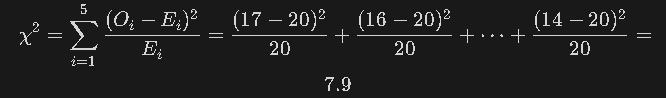
- Oi: 관찰값(observed)
- Ei: 기대값(expected)
검정 결과 해석
** 왜 자유도가 k-1 인지?
통계에서 자유도란? What Are Degrees of Freedom in Statistics?
매니저님 답변 :
자유도란? : 자유롭게 값을 선택할 수 있는 독립적인 요소의 개수
왜 K−1인가? : 평균 등의 제약 조건 때문에 마지막 값이 자동으로 결정되기 때문!
실생활 예시: 예산을 정할 때, 총 금액이 고정되어 있다면 일부 지출은 자유롭게 조정할 수 있지만, 마지막 금액은 자동으로 결정됨.
- 범주가 5개(딸기맛, 소다맛, 고추맛, ... )이므로 자유도(df) = 5 - 1 = 4 # k-1은 범주의 갯수
- 유의수준(5%)에서의 임계값

- 계산된 검정통계량(7.9)이 임계값(9.4877)보다 작으므로, 귀무가설(“균등 비율로 섞여 있다”)을 기각하기 어렵다고 판단.
- 즉, “유의한 차이가 없다”고 보아, 실제 관찰빈도와 기대빈도가 통계적으로 크게 다르지 않다고 결론 내린다.
교차분석 예시 및 기대빈도 계산 방법
교차분석(독립성 검정) 개요
- 두 개 이상의 범주형 변수가 서로 관련성이 있는지(독립이 아닌지)를 알아보는 방법.
- 예: 남학생·여학생(범주1) × 짜장면·짬뽕·마라탕(범주2)으로 구성된 2차원 분할표(contingency table)를 구성해, 각 셀의 관찰빈도와 기대빈도 사이의 차이가 통계적으로 유의한지를 카이제곱 검정으로 확인.
기대빈도(Expected Frequency) 계산 공식
- 보통 각 셀의 기대빈도는 다음과 같이 구합니다:
(행의 합) × (열의 합) / (전체 합)\text{(행의 합) × (열의 합)} \;\big/\;\text{(전체 합)}
- 예를 들어,
- 남학생 전체가 40명, 짜장면 선택이 37명, 전체 표본이 85명이라고 할 때,
- 남학생 & 짜장면 셀의 기대빈도는

- 이렇게 구한 각 셀의 기대빈도와 실제 관측빈도를 비교해 카이제곱 통계량을 산출하고, 이 값이 임계값(또는 p-value)과 비교해서 귀무가설(“두 범주형 변수는 독립적이다”)의 기각 여부를 판단합니다.
실제 예시 표

- 괄호 안의 숫자가 기대빈도, 괄호 밖이 관측빈도입니다.
- 이 표의 각 셀에 대해 값을 구한 뒤 모두 합하면 해당 교차분석의 x^2 통계량이 됩니다.

4. 카이제곱 검정 절차
- 데이터 수집 & 분할표 작성
- 기대도수 계산
- χ2 통계량 계산
- 자유도(범주 개수-1), p-value값 확인
- 결과 해석
5. 검정 가정 & 주의사항
- 표본의 독립성: 측정된 샘플들이 서로 독립적이어야 합니다.
- 기대도수 5 이상: 각 셀의 기대도수가 5 미만인 셀이 여러 개 있으면, χ2 분포 근사가 불안정해집니다. 이 경우 셀을 합치거나 Fisher의 정확 검정 등을 고려할 수 있습니다.
- 표본 크기: 극단적으로 적은 표본은 분할표 구성 자체가 무의미해질 수 있습니다.
- 연속성 보정: 2×2 표에서 정확도를 높일 수 있음 (Yates의 연속성 보정을 적용하기도 합니다.)
- 단, 보정이 필요하다 싶으면 그냥 카이제곱 검정을 엎고 머신러닝으로 넘어가는게 좋음
6. 카이제곱 (χ2) 해석과 보고
- 독립성 검정 예시: p-값 < 0.05 → "성별에 따라 제품 선호가 유의미하게 달라진다 (독립 아님)"
- 적합도 검정 예시: p-값 < 0.05 → 기대 분포와 다른 결과가 나타났음을 의미
- 동질성 검정 예시: p-값 < 0.05 → 지역 간 선호 패턴이 다르다고 결론
💡 보고 시에는 교차표, χ2 통계량, 자유도, p-값 등을 명시하고, 어떤 범주가 특히 많이/적게 차이를 보이는지 세부 분할표로 해석해주면 좋습니다.
7. 카이제곱 (χ2) 분석의 장점과 단점
(1) 장점
- 분석이 간단하고 직관적입니다.
- 범주형 자료 전용 분석 방법입니다.
- 이해하기 쉬운 결과를 제공합니다.
(2) 단점
- 기대도수 5 이상 조건을 만족해야 합니다.
- 원인-결과 분석이 제한적입니다. (연관성만 파악)
- 집단의 세부적인 차이 파악이 어려울 수 있습니다.
8. 카이제곱 (χ2)을 실무에 적용시 고려사항
- 데이터 구조 파악: 각 범주별 관측 빈도가 충분한지, 일부 셀에 데이터가 몰려 있지 않은지 확인합니다.
- 기대도수 5 미만 셀: 셀이 여러 개면 검정 결과 왜곡 가능성이 있습니다. 셀 병합 혹은 다른 검정 (Fisher 정확 검정 등) 활용을 고려합니다.
- 결과 해석: p-값만 보지 말고, 잔차 분석을 통한 세부 해석 또는 효과 크기 (Cramer's V, Phi 계수) 도 추가로 제시하면 좋습니다.
- 표본 추출 방식: 동질성 검정 vs 독립성 검정 구분 시, 사전에 표본 추출 방식 및 연구 설계를 명확히 정의해야 합니다.
- 파이썬 코드 확인하기 ( 통계학 기초 내용이랑 동일!)
1) 적합성 검정 (Goodness-of-fit test)- 문제 상황 예시: 3가지 범주(예: 색상 빨강/초록/파랑)가 일정 비율로 분포한다고 이론적으로 기대하지만, 실제 관측된 빈도가 그와 맞는지 확인
- 함수: scipy.stats.chisquare(observed, f_exp=expected)
- 주의: 실제로 “독립성 검정”과 “동질성 검정”은 동일한 통계 기법(chi2_contingency)**을 이용
- 독립성 검정은 “하나의 모집단에서 두 범주형 변수가 서로 독립인지”를 묻고,
- 동질성 검정은 “두 개 이상의 다른 모집단(집단)에서 어떤 범주(분포)가 동일(동질)한지”를 묻습니다. 코드 구현과 수식은 같으나, 해석과 자료 수집 방식이 다를 뿐임을 참고하세요.
import numpy as np
from scipy.stats import chisquare
# 관측값(Observed)
observed = np.array([18, 22, 30])
# 기대값(Expected) - 예: 빨강 20, 초록 20, 파랑 30 정도로 가정
expected = np.array([20, 20, 30])
# 적합성 검정
chi2_val, p_val = chisquare(observed, f_exp=expected)
print("[적합성 검정]")
print(f"Chi-square statistic: {chi2_val:.3f}")
print(f"p-value: {p_val:.3f}")
# p-value가 0.05보다 작으면 -> '기대분포와 유의하게 다르다' (귀무가설 기각)
2) 독립성 검정 (Independence test)
- 문제 상황 예시: 하나의 모집단에서 범주형 변수 A(예: 성별 = 남/여)와 범주형 변수 B(예: 메뉴 = 짜장면/짬뽕/마라탕)가 서로 독립인지 확인
- 함수: scipy.stats.chi2_contingency(2차원 분할표)
import numpy as np
from scipy.stats import chi2_contingency
# 예시 데이터: 한 학교에서 남학생/여학생이
# 짜장면/짬뽕/마라탕 중 어떤 메뉴를 선택했는지 관측 빈도표(2행x3열)
obs_table = np.array([
[21, 13, 6], # 남학생
[16, 15, 14], # 여학생
])
chi2_val, p_val, dof, expected_table = chi2_contingency(obs_table)
print("[독립성 검정]")
print(f"Chi-square statistic: {chi2_val:.3f}")
print(f"p-value: {p_val:.3f}")
print(f"Degrees of freedom: {dof}")
print("[각 셀의 기대빈도표]")
print(expected_table)
# p-value가 0.05보다 작으면 -> '성별과 메뉴 선택은 독립이 아님' (귀무가설 기각)
# 그렇지 않으면 -> '독립적이다' (귀무가설 채택)
3) 동질성 검정 (Test of homogeneity)
- 문제 상황 예시: 서로 다른 모집단(예: 지역 A/B/C)에 대해, 어떤 범주(예: 메뉴 3종류) 분포가 **같은지(동질)**를 확인.
- 역시 chi2_contingency 함수를 사용하되, **각 행(또는 열)**이 “서로 다른 모집단”으로 간주됩니다.
import numpy as np
from scipy.stats import chi2_contingency
# 예시 데이터: 지역 A, B, C (3개 집단)에서
# 메뉴 3종(짜장면/짬뽕/마라탕) 선택 인원 관측 빈도
obs_table_homogeneity = np.array([
[30, 20, 50], # 지역 A
[35, 25, 40], # 지역 B
[45, 30, 25], # 지역 C
])
chi2_val_h, p_val_h, dof_h, expected_table_h = chi2_contingency(obs_table_homogeneity)
print("[동질성 검정]")
print(f"Chi-square statistic: {chi2_val_h:.3f}")
print(f"p-value: {p_val_h:.3f}")
print(f"Degrees of freedom: {dof_h}")
print("[각 셀의 기대빈도표]")
print(expected_table_h)
# p-value가 0.05보다 작으면 -> '세 지역의 메뉴 선호 분포가 동일하지 않다' (귀무가설 기각)
# 크면 -> '분포가 동질적(같다)' (귀무가설 채택)
9. Python 예시 코드 (독립성 검정)
import numpy as np
import pandas as pd
from scipy.stats import chi2_contingency
from math import sqrt
# ------------------------------------------------
# 1) 예시 데이터 (관측도수 표: 2행 x 3열)
# ------------------------------------------------
# 예) 도시 A (행1), 도시 B (행2)
# 카테고리 3개 (열1, 열2, 열3)
obs = np.array([[10, 15, 25], # 도시 A의 분포
[20, 25, 5]]) # 도시 B의 분포
# 행/열 이름을 붙여보고 싶다면 DataFrame으로 관리:
df_obs = pd.DataFrame(obs,
index=['City_A','City_B'],
columns=['Prefer_1','Prefer_2','Prefer_3'])
print("== 관측도수(Observed Frequencies) ==")
print(df_obs, "\n")
# ------------------------------------------------
# 2) 카이제곱 독립성 검정
# ------------------------------------------------
chi2, p, dof, expected = chi2_contingency(obs)
print("== 카이제곱 검정 결과 ==")
print(f"Chi2 통계량: {chi2:.4f}")
print(f"p-value: {p:.4f}")
print(f"자유도(df): {dof}")
df_expected = pd.DataFrame(expected,
index=['City_A','City_B'],
columns=['Prefer_1','Prefer_2','Prefer_3'])
print("\n[기대도수(Expected Frequencies)]")
print(df_expected)
# 유의수준 설정 (예: 0.05)
alpha = 0.05
if p < alpha:
print("\n=> 귀무가설 기각: 통계적으로 유의한 연관성이 있다고 판단합니다.")
else:
print("\n=> 귀무가설 채택: 유의한 연관성을 찾지 못했습니다.")
# ------------------------------------------------
# 3) 잔차(Residual) 분석
# ------------------------------------------------
# 표준화 잔차: (관측값 - 기대값) / sqrt(기대값)
std_res = (obs - expected) / np.sqrt(expected)
df_std_res = pd.DataFrame(std_res,
index=['City_A','City_B'],
columns=['Prefer_1','Prefer_2','Prefer_3'])
print("\n== 표준화 잔차(standardized residuals) ==")
print(df_std_res)
# 특정 기준(예: ±1.96) 이상이면 통계적으로 유의하게 기대보다 많거나 적다는 해석 가능
sig_mask = np.abs(std_res) > 1.96
df_sig_mask = pd.DataFrame(sig_mask,
index=['City_A','City_B'],
columns=['Prefer_1','Prefer_2','Prefer_3'])
print("\n[잔차 > ±1.96 여부]")
print(df_sig_mask)
# ------------------------------------------------
# 4) 효과크기: Cramer's V
# ------------------------------------------------
# Cramer's V = sqrt( (chi2 / n) / (k-1) )
# - n: 전체 표본 크기
# - k: min(행-1, 열-1)
n = obs.sum()
phi2 = chi2 / n
r, c = obs.shape
k = min(r-1, c-1) # 독립성 검정에서는 (행-1, 열-1) 중 작은 값
cramers_v = sqrt(phi2 / k)
print(f"\n== Cramer's V (효과크기) ==")
print(f"Cramer's V: {cramers_v:.4f}")
10. Cramer's V 란?
카이제곱 검정에서 두 범주형 변수 간의 연관성을 측정하는 값입니다. 📊 즉, 두 변수가 얼마나 강하게 관련되어 있는지 수치로 보여주는 지표입니다.
왜 Cramer's V 를 사용할까요?
카이제곱 검정은 두 변수 간에 연관성이 있는지 여부만 알려줍니다. 하지만 Cramer's V 를 사용하면 연관성의 강도까지 파악할 수 있습니다. 💪
Cramer's V 는 어떻게 계산할까요?
다음과 같은 공식을 사용합니다.
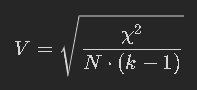
- χ2: 카이제곱 검정 통계량
- N: 총 관측값의 개수
- k: 행 (row) 또는 열 (column) 의 작은 쪽 범주 개수
11. Cramer's V 값은 어떻게 해석할까요?
Cramer's V 값은 0 에서 1 사이의 값을 가지며, 값이 클수록 연관성이 강합니다.
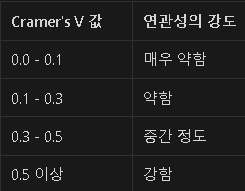
주의: 연관성의 강도를 해석할 때는 데이터의 맥락과 범주 개수를 고려해야 합니다.
12. Cramer's V 계산 예시
데이터: 한 제조업체에서 생산 라인 (A, B, C) 과 제품 상태 (양품, 불량) 간의 관계를 분석하려고 합니다. 아래 교차표를 바탕으로 카이제곱 검정을 수행했습니다.

카이제곱 검정을 통해 χ2=6.5 라고 나왔다고 가정합니다.
계산

- χ2=6.5
- N=120 (총 관측값)
- k=2 (열의 범주 수: 양품, 불량)

해석
V=0.23 이므로, 두 변수 간의 연관성은 약한 수준입니다. 즉, 생산 라인과 제품 상태 간의 관계가 강하지 않다고 해석할 수 있습니다.
문제 상황과 통계 기법
1. 카이제곱 - 적합성 검정 (Goodness-of-fit)
어느 양말 공장에서는 5가지 색상(흰색, 검정, 회색, 파랑, 빨강)의 양말을 같은 비율(각 20%)로 생산한다고 광고한다.
무작위로 200켤레를 뽑아 색상을 조사했더니, 실제 빈도는 각각 42, 45, 38, 40, 35켤레였다.
이 공장에서 주장한 색상 비율(20%씩)이 실제 관측된 분포와 유의미하게 다른지 확인하고자 한다.
사용 기법: 카이제곱 적합성 검정(scipy.stats.chisquare)
2. 카이제곱 - 적합성 검정 (Goodness-of-fit)
과자 회사 A는 “새로 출시한 미니쿠키 안에 초콜릿 칩 10개, 화이트 초콜릿 칩 5개, 크랜베리 칩 5개가 항상 들어간다”고 홍보한다.
실제로 20봉지를 개봉해 각 칩 종류별 갯수를 세었더니, 평균 9.5개, 6개, 4.5개로 조사되었다.
회사 측 주장(10:5:5 비율)과 실제로 들어 있는 칩 비율이 일치하는지 통계적으로 검정하고자 한다.
사용 기법: 카이제곱 적합성 검정
3. 카이제곱 - 독립성 검정 (Independence)
한 대학교 학생들을 대상으로 **전공 계열(인문사회, 자연공학, 예체능)**과 **선호하는 공부 장소(도서관, 카페, 집)**를 조사하여, 전공과 장소 선호가 독립적인지 알아보고자 한다.
사용 기법: 카이제곱 독립성 검정(scipy.stats.chi2_contingency)
4. 카이제곱 - 독립성 검정 (Independence)
한 쇼핑몰에서 **멤버십 등급(실버, 골드, 플래티넘)**과 **주 1회 이상 구매 여부(한다/안 한다)**가 관련이 있는지 궁금하다.
3×2 교차표(등급별로 “구매” vs “미구매” 횟수)를 구성하여 두 범주형 변수가 독립인지 조사한다.
사용 기법: 카이제곱 독립성 검정
5. 카이제곱 - 동질성 검정 (Homogeneity)
제조 공장이 3곳(A, B, C) 있는데, 모두 동일한 제품(휴대폰 케이스)을 만든다.
각 공장에서 랜덤 샘플 100개씩을 추출하여 불량 원인(스크래치, 찢어짐, 색 번짐, 기타) 분포가 서로 동질(동일)한지 확인하려고 한다.
사용 기법: 카이제곱 동질성 검정(scipy.stats.chi2_contingency)
- 여기서는 “A/B/C 3개 공장”이 서로 다른 모집단을 의미하고, “불량 원인”이 단일 범주형 변수.
6. 카이제곱 - 동질성 검정 (Homogeneity)
패스트푸드점 3개 브랜드(M사, B사, K사)의 매장 10곳씩을 방문하여, 방문 고객 100명을 무작위로 조사했다.
“선호 메뉴(버거, 치킨, 사이드류)” 분포가 브랜드마다 같은지(동질한지) 알아보려고 한다.
사용 기법: 카이제곱 동질성 검정
7. 카이제곱 - 독립성 vs 동질성 차이 예시
(개념 이해용)
- 독립성 검정: 한 도시의 시민 전체(단일 모집단)에서 **‘직업군(사무직, 서비스직, 전문직 등)’ vs ‘운동 취미 종류(헬스, 수영, 골프, 없음 등)’**가 독립인가?
- 동질성 검정: **도시가 다른 3개 지역(서울, 부산, 광주)**에서, 사무직·서비스직·전문직 분포가 동일한지?
두 경우 모두 카이제곱 분할표로 검정하지만, “하나의 모집단 내부 두 범주의 독립성”과 “서로 다른 모집단(도시) 간 단일 범주의 분포 동질성”이라는 맥락 차이가 있다.
사용 기법: 모두 chi2_contingency 활용, 해석이 다름
8. 선형회귀 - 단순선형회귀(Simple Linear Regression)
한 쇼핑몰에서 **광고비(만원 단위)**를 x, **하루 매출(만원 단위)**을 y로 잡고, 광고비가 매출에 미치는 영향을 예측하고자 한다.
사용 기법: 단순선형회귀(예: statsmodels나 sklearn.linear_model.LinearRegression)
9. 선형회귀 - 단순선형회귀
초등학교 인근 가게에서 **기온(℃)**에 따라 아이스크림 판매 개수가 어떻게 달라지는지 조사하여, 기온(x)과 판매량(y)의 상관 및 예측 모델을 만들었다.
사용 기법: 단순선형회귀
10. 선형회귀 - 다중선형회귀(Multiple Linear Regression)
아파트 가격을 예측하기 위해, 독립변수로 “평수, 층수, 역까지 거리, 주변 학군 평판 지수” 등을 고려하고,
종속변수로 “아파트 실거래가(만원)”를 설정하여 회귀 모델을 구축한다.
사용 기법: 다중선형회귀(예: sklearn.linear_model.LinearRegression)
11. 선형회귀 - 다중선형회귀
스타트업에서 직원들의 생산성 점수(예: 단위시간당 처리 업무량)를 예측하기 위해,
“주당 근무시간, 재택근무 여부(더미 변수로 변환), 직무만족도, 팀 내 커뮤니케이션 점수” 등을 예측 변수로 사용하는 모델을 개발하려 한다.
사용 기법: 다중선형회귀
12. ANOVA(일원분산분석) - One-Way ANOVA
- *세 가지 교육 방식(A, B, C)**을 무작위로 배정받은 학생 집단(각 20명씩)의 기말시험 점수를 비교하여, 교육 방식 간 평균 점수가 통계적으로 차이가 있는지 알아본다.
사용 기법: 일원분산분석(One-way ANOVA)
13. ANOVA(일원분산분석) - One-Way ANOVA
어느 제과점에서 효모 A, B, C를 사용해 빵을 구웠을 때의 “팽창률”이 서로 차이가 나는지 확인하고 싶다.
효모 종류(집단)별로 샘플 10개씩 테스트하여 평균 팽창률을 비교한다.
사용 기법: 일원분산분석
14. ANOVA(이원분산분석) - Two-Way ANOVA
한 식당에서 **조리 방법(프라이, 찜)**과 **소스 종류(매운맛, 순한맛)**라는 두 개의 요인(독립변수)이, 음식의 “맛 점수(5점 척도)”에 어떤 영향을 미치는지 보고 싶다.
사용 기법: 이원분산분석(Two-Way ANOVA)
- (요인1) 조리 방법 2수준, (요인2) 소스 2수준 → 2×2 구성이며, 상호작용 효과도 확인 가능
15. ANOVA(이원분산분석) - Two-Way ANOVA
연구자가 **운동 프로그램(필라테스, 요가, 웨이트)**와 **식단 유형(고단백, 저탄수, 일반)**이라는 두 요인이 **체중 감소(kg)**에 미치는 영향 및 상호작용을 조사.
사용 기법: 이원분산분석
16. 로지스틱 회귀 - 이진 로지스틱 회귀(Binary Logistic Regression)
한 은행에서 **대출 승인 여부(승인=1, 거절=0)**를 예측하기 위해, “신용점수, 연소득, 자산 규모, 부채율” 등을 독립변수로 하는 모델을 만든다.
사용 기법: 이진 로지스틱 회귀(sklearn.linear_model.LogisticRegression 등)
17. 로지스틱 회귀 - 이진 로지스틱 회귀
인터넷 쇼핑몰에서 구매 완료(1) vs 장바구니 담기만 함(0) 여부를 예측하고자,
“제품 가격, 할인 쿠폰 사용 여부, 최근 방문 횟수, 회원 등급” 등을 예측 변수로 설정했다.
사용 기법: 이진 로지스틱 회귀
18. 로지스틱 회귀 - 다항 로지스틱 회귀(Multinomial Logistic)
자동차 보험사에서 사고 유형을 “경미(0), 중간(1), 심각(2)” 3단계로 분류해 놓았고, 이를 예측하기 위해 “운전 경력, 차종, 사고 경력, 나이” 등을 설명 변수로 사용한다.
사용 기법: 다항 로지스틱 회귀(Multinomial Logistic Regression)
19. 로지스틱 회귀 - 다항 로지스틱 회귀
한 식품 기업에서 소비자들의 선호 패키지 디자인(A/B/C 중 택1)을 예측하기 위해, “연령대, 성별, 브랜드 로열티 지수, 패키지 컬러 선호도 점수” 등을 독립변수로 사용한다.
사용 기법: 다항 로지스틱 회귀
20. 로지스틱 회귀 vs 선형회귀 비교 문제
어떤 벤처 회사에서 신규 서비스를 개발하며,
- (로지스틱 회귀) “초기 클로즈 베타 유저들이 정식 출시 후에도 계속 서비스에 잔류할지(1) 중단할지(0)”를 예측하는 모델,
- (선형회귀) “잔류 유저들의 월평균 결제금액을 예측”하는 모델 두 가지를 동시에 구축하고자 한다.
잔류 여부는 이진 분류 → 로지스틱 회귀결제금액은 연속값 예측 → 선형회귀
오늘의 요약
- 카이제곱 검정
- 적합성 검정: 단일 범주의 “관찰분포 vs 이론(기대)분포” 비교
- 독립성 검정: 하나의 모집단 내 두 범주형 변수의 독립성 판단
- 동질성 검정: 여러 모집단에서 하나의 범주형 변수의 분포가 같은지 비교
- 선형회귀
- 종속변수가 연속형일 때, 독립변수들과의 관계를 추정
- 단순(1개 독립변수) vs 다중(여러 독립변수)
- ANOVA(분산분석)
- 범주형 독립변수(집단)에 따른 연속형 종속변수(평균차이) 분석
- 일원(1개 요인) vs 이원(2개 요인, 상호작용 포함)
- 로지스틱 회귀
- 종속변수가 범주형(이진 또는 다항)일 때 사용
- 이진 로지스틱(0/1) vs 다항 로지스틱(3개 이상의 범주)
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
코드카타

signs 가 지나갈 때 참이면 absolutes 는 그대로 가고 땡이면 음수 붙여주고 나중에 변환된 absolutes 총 합 구하면 되네
오답
---> 11 solution([4,7,12],[true,false,true])
NameError: name 'true' is not defined
넣었을 때 true 못 찾아냄 -> str 타입 변환 필요해보임
이것도 똑같이 안된다함 str 타입 변환이 아닌가본데?
애초에 signs는 불리언 타입이니까 0/1 로 나눠줘야하나? 아닌데;
이것도 안된다하네 ? 이런 ㅎㅎㅎㅎ
흠 답 좀 까볼게요 gg
아니 이거 왜 되는데요???????? true 못 찾는다매 false는 왜 False 그대로 보냐고 !!
다른 사람 풀이
def solution(absolutes, signs):
return sum(absolutes if sign else -absolutes for absolutes, sign in zip(absolutes, signs))
캬 짧다
람다 든 캄프리헨션이든 뭐든 배우자 ..
'본 캠프 TIL' 카테고리의 다른 글
| 1월 23일 TIL 머신러닝 오프닝 2회차, 통계학 세션 막회차, 코드카타 (2) | 2025.01.23 |
|---|---|
| 1월 22일 TIL 머신러닝 기초~선형회귀,머신러닝 1회차, 통계학 5회차 세션 (4) | 2025.01.22 |
| 1월 20일 TIL 통계학 라이브 세션 3회차, 5,6주차, 마쉰라닝 기초 겉핥기, 코드카타, 아티클 (0) | 2025.01.20 |
| 1월 17일 TIL 통계학 3,4주차, 라이브 세션, 코드카타 (0) | 2025.01.17 |
| 1월16일 TIL 라이브 세션, 통계학 1&2주차, 코드카타, 아티클 스터디 (0) | 2025.01.16 |